Let mass of plate per unit area \(=\) \(\mathrm{m}\)
\( = {M_1} = \pi {\left( {\frac{{56}}{2}} \right)^2}m = \pi {\left( {28} \right)^2}m\)
\( = {M_1} = \pi {\left( {\frac{{42}}{2}} \right)^2}m = \pi {\left( {21} \right)^2}m\)
Mass of remaining Part \(=\) \(M-M_{1}\)
\(C.M\) of whole disc \(=\mathrm{O}\) i.e at origin
\(C.M\) of removed Plate \(=r_{1}=28-21=7 \mathrm{cm}\)
\(C.M\) of remaining Portion \(=\mathrm{r}_{2}\)
hence
\(\mathrm{M} \times \mathrm{O}=\mathrm{M}_{1} \mathrm{r}_{1}+\left(\mathrm{M}-\mathrm{M}_{1}\right) \mathrm{r}_{2}\)
\(\mathrm{M}_{1} \mathrm{r}_{1}=-\left(\mathrm{m}-\mathrm{m}_{1}\right) \mathrm{r}_{2}\)
\({r_2} = \left[ {\frac{{\left( {{M_1}{r_1}} \right)}}{{ - \left( {m - {m_1}} \right)}}} \right]\)
\( = \left[ {\frac{{\pi {{\left( {21} \right)}^2}m}}{{ - \pi {{\left( {28} \right)}^2} - \pi {{\left( {21} \right)}^2}m}}} \right] \times 7\)
\( = \left[ {\frac{{{{\left( {21} \right)}^2}}}{{\left( { - 343} \right)}}} \right] \times 7\)
\(r_{2}=-9 \mathrm{cm}\)
Download our appand get started for free
Similar Questions
- 1ચાકગતિ કરતાં બે પદાર્થો $A$ અને $B$ ના દ્રવ્યમાન $m $ અને $2m$ જેની જડત્વની ચાકમાત્રા $I_A$ અને $ I_B (I_B>I_A)$ અને ચાકગતિ ઊર્જાઓ સમાન છે. જો તેમના કોણીય વેગમાન અનુક્રમે $L_A$ અને $L_B$ હોય, તો .....View Solution
- 2પ્રત્યેકનું દળ $1 \mathrm{~kg}$ હોય તેવા ચાર કણોને $2 \mathrm{~m}$ બાજુ ધરાવતા ચોરસના ચાર ખૂણા પર મૂકેલા છે. તેના એક શિરોબિંદુમાંથી પસાર થતી અને સમતલને લંબ અક્ષને અનુલક્ષીને તંત્રની જડત્વની ચાક્માત્રા______$\mathrm{kg} \mathrm{m}^2$છે.View Solution
- 3સમાન તારમાંથી $P$ અને $Q$ રીંગ બનાવવામાં આવે છે.તેમની ત્રિજયા $r$ અને $nr$ છે. $Q$ ની જડત્વની ચાકમાત્રા $P$ કરતાં $8$ ગણી હોય,તો $n$ કેટલો હશે?View Solution
- 4એક દઢ પદાર્થના બે કણોના સ્થાનસદિશ $(3, 0, 0)\ m $ અને $ (0, 3, 0)\ m$ છે. આ કણો પર $ (0, 1, 0) \ N$ અને $(0, -1, 0)\ N $ બળો લાગે છે, તો બળયુગ્મની ચાકમાત્રા ....... $Nm$ હશે.View Solution
- 5$M$ દળ અને $R$ ત્રિજ્યા ધરાવતી એક પાતળી વર્તુળાકાર રીંગ સમક્ષિતિજ સમતલમાં, સમતલને લંબ અક્ષને અનુલક્ષીને $2 \,rads^{-1}$ ના કોણીય વેગથી ભ્રમણ કરે છે. જો બે સમાન $m$ દળ વાળા પદાર્થોને હળવેકથી રિંગના વ્યાસના વિરુધ્ધ છેડાઓ જોડવામાં આવે તો હવે રીંગ .............. ( $rads^{-1}$ માં) ના કોણીયવેગ સાથે પરિભ્રમણ કરશે.View Solution
- 6એક ધન ગોળો $A $ અને બીજા પોલા ગોળા $B$ નું દળ સમાન અને બાહ્ય ત્રિજ્યા સમાન છે. તેમના વ્યાસ પર જડત્વની ચાકમાત્રા $I_A$ અને $I_B$ હોય, તો ...... જ્યાં $ A$ અને $B$ તેમની ઘનતા છે.View Solution
- 7View Solutionઢોળાવવાળા સમતલ પર અમુક ઉંચાઈ નળાકાર ચઢે છે અને પછી ગબડીને નીચે આવે છે. (સમગ્ર ગતિ દરમિયાન સરકતો નથી.) નળાકાર પર લાગતા ઘર્ષણ બળની દિશા કઈ છે.
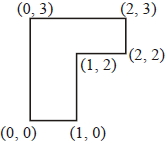
- 8આપેલ ઝંડા આકારની પાતળી તકતીનું દળ $4\;kg$ છે તો તેના દ્રવ્યમાન કેન્દ્રના યામ શું થશે?View Solution
- 9બે સરખા બોલ આકૃતિમાં દર્શાવ્યા મુજબ એક હળવા દઢ સળિયાથી જોડેલા છે. જો $J-=Mv$ એક બોલ પર લગાડવામાં આવે તો તેનો કોણીય વેગ કેટલો થાય ?View Solution

- 10નીચે બે વિધાનો આપેલા છે : એક વિધાન $A$ અને બીજું કારણ $R$ વડે દર્શાવેલ છે.View Solution
વિધાન $A :$ $M$ દળ અને $R$ ત્રિજ્યા ધરાવતી વર્તુળાકાર તકતી લગભગ $X, Y$ અક્ષ (તેના પ્લેનમાંથી પસાર થતી) અને $Z-$ અક્ષ જે તેના પ્લેન પર લંબ છે તેને અનુલક્ષીને જડત્વની ચાકમાત્રા અનુક્રમે $I_{x}, I_{y}$ અને ${I}_{z}$ છે. ત્રણેય અક્ષને અનુલક્ષીને ચક્રાવર્તન ત્રિજ્યા સમાન હશે.
Reason $R$ : ચાકગતિ કરતાં દઢ પદાર્થનું દળ અને આકાર નિશ્ચિત હોય છે.
ઉપર આપેલા વિધાનો માટે નીચેનામાંથી યોગ્ય વિકલ્પ પસંદ કરો.
