ધારો કે બે પારદર્શક માધ્યમોને $x - z$ સમતલથી અલગ કરવામાં આવ્યા છે. $Z \geq 0$ માટે માધ્યમ $1$ નો વક્રીભવનાંક $\sqrt{2}$ અને $z <0$ માટ માધ્યમ $2$ નો વક્રીભવનાંક $\sqrt{3}$ છે. પ્રકાશનું કિરણ આ સમતલ પર આપાત થાય છે. જેનું સમીકરણ $\vec{ A }=6 \sqrt{3} \hat{ i }+8 \sqrt{3} \hat{ j }-10 \hat{ k }$ છે. માધ્યમ $-2$ માં આ કિરણ કેટલાના ખૂણે વક્રીભૂત થશે?
AIEEE 2011, Diffcult
Download our app for free and get started
a
Angle of incidence is given by
Angle of incidence is given by
\(\cos (\pi-i)=\frac{(6 \sqrt{3} \hat{i}+8 \sqrt{3} \hat{j}-10 \hat{k}) \hat{k}}{20}\)
\(-\cos i=-\frac{1}{2}\)
\(\angle i=60^o\)
From Snell's law, \(\sqrt{2} \sin i=\sqrt{3} \sin r\)
\(\angle r=45^o\)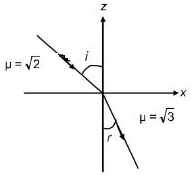
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$20$ $cm$ ના મૂલ્યની કેન્દ્રલંબાઇ ધરાવતા એક અભિસારી કાચથી $15$ $cm$ દૂર જેની કેન્દ્રલંબાઇનું મૂલ્ય $25$ $cm$ છે.તેવો એક અપસારી કાચ મૂકેલ છે,એક સમાંતર પ્રકાશપૂંજ આ અપસારી કાચ પર પડે છે.આમ રચાતું અંતિમ પ્રતિબિંબ થશે.View Solution
- 2View Solutionઆપેલ આકૃતિમાં કાંચનો વક્રીભવનાંક કેટલો થાય?
- 3ધારો કે બે પારદર્શક માધ્યમોને $x - z$ સમતલથી અલગ કરવામાં આવ્યા છે. $Z \geq 0$ માટે માધ્યમ $1$ નો વક્રીભવનાંક $\sqrt{2}$ અને $z <0$ માટ માધ્યમ $2$ નો વક્રીભવનાંક $\sqrt{3}$ છે. પ્રકાશનું કિરણ આ સમતલ પર આપાત થાય છે. જેનું સમીકરણ $\vec{ A }=6 \sqrt{3} \hat{ i }+8 \sqrt{3} \hat{ j }-10 \hat{ k }$ છે. માધ્યમ $-2$ માં આ કિરણ કેટલાના ખૂણે વક્રીભૂત થશે?View Solution
- 4અંતર્ગોળ અરીસાની કેન્દ્રલંબાઈ $30\, cm $છે. જો પ્રતિબિંબ ઊલટું (વાસ્તવિક) હોય તો, અરીસાના સામે રહેલી વસ્તુ નું સ્થાન....$cm$ અંતરે હોઈ શકે જેથી પ્રતિબિંબ વસ્તુના કદ કરતાં ત્રણ ગણું હોય.View Solution
- 5બિંદુવત પદાર્થ $24 \, cm$ કેન્દ્રલંબાઈના અંતર્ગોળ અરીસાના મુખ્ય અક્ષ પર અરીસા તરફ ગતિ કરે છે. જ્યારે તે $60\,\, cm$ અંતરે હોય ત્યારે તેનો વેગ $9 \, cm/sec$ છે તે ક્ષણે પ્રતિબિંબનો વેગ શું હશે?View Solution
- 6View Solutionએસ્ટ્રોનોમિકલ ટેલિસ્કોપનો સામાન્ય દ્રષ્ટિ માટે મેગ્નિફિકેશ પાવર સાદી રીતે ........થી આપી શકાય છે.
- 7${f_1}$ અને ${f_2}$ કેન્દ્રલંબાઇ ધરાવતા લેન્સ સંપર્કમાં હોય,ત્યારે પ્રતિબિંબ $60cm$ અંતરે મળે છે.જયારે બંને લેન્સને $10cm $ અંતરે રાખતા પ્રતિબિંબ $30cm$ અંતરે મળે છે.તો ${f_1}$ અને ${f_2}$ કેટલા થાય?View Solution
- 8$60^°$ ના ખૂણે રહેલા બે સમતલ અરીસા પર એક કિરણ $50^°$ ના ખૂણે આપાત કરવામાં આવે છે.તે પરાવર્તન પામીને બીજા અરીસા પર આપાત થાય છે.ત્યાંથી પરાવર્તન પામીને પ્રથમ અરીસા પર ......$^o$ ના ખૂણે આપાત થશે?View Solution
- 9એક તરવૈયો પાણીની અંદરથી બહારની બાજુ વર્તુળાકાર ક્ષેત્રમાં જોવે છે. પાણીનો વક્રીભવનાંક $\frac{4}{3}$ અને તરવૈયાની આંખ પાણીની સપાટીથી $15\, cm$ ઊંડાઈએ છે. તો તેને બહાર દેખાતા ક્ષેત્રના વર્તુળની ત્રિજ્યા કેટલી હશે?View Solution
- 10$3 cm$ જાડાઇ અને $3/2$ વક્રીવનાંક ધરાવતા કાંચને કાગળ પર રહેલા શાહીનું નિશાન પર મૂકવામાં આવે છે. તે નિશાનને $5 cm$ ઊંચાઇએથી જોતાં નિશાનનું પ્રતિબિંબ માણસની આંખથી કેટલા.....$cm$ અંતરે પડશે?View Solution