$\frac{2}{{\sqrt \pi }}cm$ વ્યાસ ધરાવતા નળમાથી આવતું પાણી $5\,minutes$ માં $15\,litre$ ની ડોલ ભરે તો પ્રવાહનો રેનોલ્ડ નંબર કેટલો હશે? (પાણીની ઘનતા $= 10^3\,kg/m^3$ અને પાણીનો શ્યાનતાગુણાંક $= 10^{-3}\,Pa.s$ )
JEE MAIN 2015, Diffcult
d
Given: Diameter of water tap \( = \frac{2}{{\sqrt \pi }}\,cm\)
Given: Diameter of water tap \( = \frac{2}{{\sqrt \pi }}\,cm\)
\(\therefore \,\,Radius,\,r = \frac{1}{{\sqrt \pi }} \times {10^{ - 2}}\,m\)
\(\frac{{dm}}{{dt}} = \rho AV\)
\(\frac{{15}}{{5 \times 60}} = {10^3} \times \pi {\left( {\frac{1}{{\sqrt \pi }}} \right)^2} \times {10^{ - 4}}V\)
\( \Rightarrow V = 0.05\,m/s\)
Reynold's number, \({R_e} = \frac{{\rho Vr}}{n}\)
\( = \frac{{{{10}^3} \times 0.5 \times \frac{2}{{\sqrt \pi }}{{10}^{ - 2}}}}{{{{10}^{ - 3}}}} \cong 5500\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
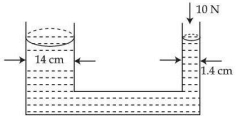
- 1આકૃતિમાં દર્શાવ્યા મુજબ ના વ્યાસ ધરાવતી બે ભુજાએમાં પાણી ભરેલું હોય તેવો હાઈડ્રોલીક પ્રેસને દર્શાવેલ છે. તેના પાતળી ભુજામાં રહેલ પાણી ઉપર $10 \mathrm{~N}$ નું બળ લગાડવામાં આવે છે. પાણીને સંતુલન સ્થિતિમાં રાખવા માટે જાડી (મોટી) ભુજામાં રહેલ પાણી ઉપર લગાવવું પડતું બળ. . . . . . $\mathrm{N}$ હશે.View Solution
- 2પાત્રના તળિયે સમાન લંબાઇ ધરાવતી $r_1$ અને $ r_2$ ત્રિજયાવાળી કેશનળી જોડેલ છે.તો કેટલી ત્રિજયાની કેશનળી જોડવાથી પ્રવાહ અચળ રહે?View Solution
- 3જ્યારે બ્લોક હવામાં હોય ત્યારે સ્પ્રિંગ માપન $60 \,N$ છે. જ્યારે તેને પાણીની અંદર નાખવામાં આવે ત્યારે તેનું માપન $40 \,N$ છે. તો બ્લોકનું વિશિષ્ટ ઘનતા કેટલું ?View Solution
- 4અનિયમિત આડછેદ ધરાવતી પાઇપમાં બે બિંદુએ ત્રિજયાનો ગુણોત્તર $3:2$ છે.તો વેગનો ગુણોત્તર કેટલો થાય?View Solution
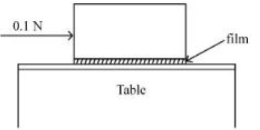
- 5આકૃતિમાં દર્શાવ્યા અનુસાર $0.20\,m ^2$ ના બેઝ (તળીયા) નું ક્ષેત્રફળ ધરાવતા એક ધાતુના ચોસલાને ટેબલ ઉપર મૂકવામાં આવેલ છે. એક $0.25\,mm$ ની પ્રવાહીની કપોટીને બ્લોક (ચોસલું) અને ટેબલની વચ્યે દાખલ કરવામાં આવે છે. બલોકને $0.1\,N$ ના સમક્ષિતિજ બળ વડે ખેંચવામાં આવે છે અને તે અચળ ઝડપથી ગતિ કરે છે. જો પ્રવાહીની સ્નિગ્ધતા $5.0 \times 10^{-3}\;Pa-s$ હોય તો બ્લોકની ઝડપ (લગભગ) $...........\times 10^{-3}\,m / s$ હશે.View Solution
- 6હાઈડ્રોલિક લિફ્ટ મહતમ $3000\, kg$ દળની કારને ઊંચકી શકે છે. લોડ ઉઠાવતો પિસ્ટનનો આડછેદ $425$ સેમી$^{2}$ છે. નાનો પિસ્ટન કેટલું મહતમ દબાણ સહન કરી શકે?View Solution
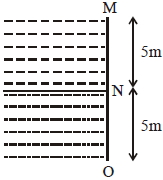
- 7આકૃતિમાં દર્શાવ્યા મુજબ $10\; \mathrm{m}$ ના ચોરસ પાત્રમાં બે પ્રવાહી ભરેલા છે જેમની ઘનતા $\rho_{1}$ અને $\rho_{2}\left(\rho_{2}=2 \rho_{1}\right)$ છે.બંને પ્રવાહીની ઊંચાઈ $5 \;\mathrm{m} .$ છે.આ પ્રવાહીના કારણે $MN$ અને $NO$ પર લાગતા બળનો ગુણોત્તર કેટલો મળે?View Solution
(પ્રવાહી એકબીજામાં મિશ્ર થતાં નથી)
- 8View Solutionનળાકાર નળીમાં ધટ્ટ પ્રવાહીનું વહન થાય છે.પ્રવાહીનો વેગ કઇ આકૃતિ મુજબ હોય .
- 9સ્ટોક્સના નિયમની સકાચણી કરવા માટે કરેલા પ્રયોગમાં $r$ ત્રિજ્યા અને $\rho$ ઘનતા ધરાવતા એક ગોળ દડાને પાણી ભરેલા પાત્રમાં પાણીની સપાટીથી $h$ ઊંચાઈ પરથી મુક્ત કરવામાં આવે છે. જો પાણીની અંદર દડાનો ટર્મિનલ વેગ એ પાણીની અંદર આવતા પહેલા દડાના વેગ જેટલો હોય તો ઊંચાઈ $h$ કોના સમપ્રમાણમાં હશે? (હવાનો શ્યાનતાગુણાંક અવગણો)View Solution
- 10$1 \;\mathrm{m}$ લંબાઈ ધરાવતા એક નળાકારને એવી ધાતુમાથી બનાવેલ છે કે જેનો રેખીય પ્રસરણાંક ખૂબ નાનો છે તેને $0^{\circ} \mathrm{C}$ તાપમાને રહેલ પાણીની સપાટી ઉપર મુક્તા તેની $20\; \mathrm{cm}$ લંબાઈ સપાટીથી ઉપર રહે છે.જ્યારે પાણીનું તાપમાન વધીને $4^{\circ} \mathrm{C}$ થાય ત્યારે નળાકારની $21 \;\mathrm{cm}$ લંબાઈ સપાટીથી ઉપર રહે છે, તો $\mathrm{T}=4^{\circ} \mathrm{C}$ એ $\mathrm{T}=0^{\circ} \mathrm{C}$ ની સાપેક્ષે ઘનતા લગભગ કેટલી થાય?View Solution
