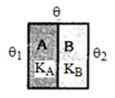
દિવાલના બે સ્તર $A$ અને $B$ જુદા જુદા પદાર્થના બનેલા છે. બંને સ્તરની જાડાઈ સમાન છે. $A,$ $K_A = 3 K_B$ છે. ઉષ્મીય સંતુલન દિવાલના છેડે તાપમાનનો તફાવત $20°C$ છે. $A$ ના છેડે તાપમાનનો તફાવત ..... $^oC$ શોધો.

Medium
d
આપેલી પરિસ્થિતિ \(\,\frac{Q}{t}\,\, = \,\,\frac{{KA\,\,({\theta _1} - {\theta _2})}}{\ell }\,\, = \,\,\) અચળ \( \Rightarrow \,\,\frac{{{K_A}A\,({\theta _1} - \theta )}}{\ell }\,\, = \,\,\frac{{{K_B}A\,\,(\theta - {\theta _2})}}{\ell }\)
આપેલી પરિસ્થિતિ \(\,\frac{Q}{t}\,\, = \,\,\frac{{KA\,\,({\theta _1} - {\theta _2})}}{\ell }\,\, = \,\,\) અચળ \( \Rightarrow \,\,\frac{{{K_A}A\,({\theta _1} - \theta )}}{\ell }\,\, = \,\,\frac{{{K_B}A\,\,(\theta - {\theta _2})}}{\ell }\)
\(\frac{{{K_A}}}{{{K_B}}}\,\, = \,\,\frac{{\theta - {\theta _2}}}{{{\theta _1} - \theta }}\,\, = \,\,3\,\,\,\, \Rightarrow \,\,3\,{\theta _1} + {\theta _2} = \,\,4\,\theta \)
\(\because \,\,\,{\theta _1} - {\theta _2} = \,\,{20^ \circ }C\,\,\,\,\,\,\)
\(\therefore \,\,\,{\theta _2} = {\theta _1} - {20^ \circ }C\,\,\,\,\)
\( \Rightarrow \,\,3\,{\theta _1} + {\theta _1} - {20^ \circ }C\,\, = \,\,4\,\theta \,\,\,\,\,\,\, \)
\(\Rightarrow \,\,4\,\,({\theta _1} - \theta )\,\, = \,\,{20^ \circ }C\,\,\,\)
\(\Rightarrow \,\,{\theta _1} - \theta \,\, = \,\,{5^ \circ }C\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1બે સમાન ધાતુના ગોળાની ત્રિજ્યાઓ $r$ અને $2r $ છે. તેને સમાન તાપમાને ગરમ કરવામાં આવે અને સમાન પરિસરમાં મૂકવામાં આવે છે. તેમના તાપમાનના ઘટાડાનો દર ગુણોત્તર .....થશે.View Solution
- 2ગરમ સૂપ ભરેલું બાઉલ (પાત્ર) જ્યારે ઓરડાનું તાપમાન $22^{\circ}\,C$ હોય ત્યારે $2$ મિનિટમાં $98^{\circ}\,C$ થી $86^{\circ}\,C$ સુધી ઠરે છે. તંને $75^{\circ}\,C$ થી $69^{\circ}\,C$ તાપમાને ઠરતા $...........$મિનીટ સમય લાગશે.View Solution
- 3ગરમ પાણીથી ભરેલા બીકરને રૂમમાં રાખવામાં આવે છે. જો તેનું તાપમાન $80^{\circ} C$ થી $75^{\circ} C\;t_1$ મિનિટમાં, $75^{\circ} C$ થી $70^{\circ} C\;t_2$ મિનિટમાં અને $70^{\circ} C$ થી $65^{\circ} C\;t_3$ મિનિટમાં થાય, તો .....View Solution
- 4થરમોસના ઢાંકણનું ક્ષેત્રફળ $75 cm^2$ અને જાડાઇ $5 cm$ છે.તેની ઉષ્મા વાહકતા $0.0075 cal/cm\,sec^oC$ છે.જો ઉષ્માનું વહન માત્ર ઢાંકણ દ્વારા થતું હોય,તો $500 gm$ $0^oC$ તાપમાને રહેલા બરફનું રૂપાંતર $0^oC$ તાપમાનવાળા પાણીમાં કરતાં ........ $(hr)$ સમય લાગશે ? બહારનું $40^oC$ તાપમાન છે,અને બરફની ગલનગુપ્ત ઉષ્મા $80 cal g^{-1}$છે.View Solution
- 5બે ગોળાઓ $P$ અને $Q$ સમાન રંગના અને તેની ત્રિજ્યા અનુક્રમે $8\,\, cm$ અને $2\,\, cm$ તેમને અનુક્રમે અને $127°C$ અને $ 527°C$ તાપમાને રાખેલા છે તો $P$ અને $Q $ ની વિકિરણ ઉર્જાનો ગુણોત્તર શોધો.View Solution
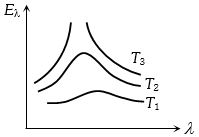
- 6View Solutionસૂર્ય, બલ્બમાં રહેલ ટંગસ્ટન ફિલામેન્ટ અને વેલ્ડિંગ આર્ક માટે વિકિરણ ઉર્જા અને તરંગલંબાઈનો ગ્રાફ આપેલ છે.તો નીચેનામાથી ક્યો વિકલ્પ સાચો પડે?
- 7$200 \,K$ તાપમાને રહેલા પદાર્થમાંથી નીકળતા તરંગની મહત્તમ તરંગલંબાઇ $14\,\mu m$ છે, જો પદાર્થનું તાપમાન $1000 \,K$ કરતાં મહત્તમ તરંગલંબાઇ મેળવો.View Solution
- 8જ્યારે ઓરડાનું તાપમાન $20^{\circ} \mathrm{C}$ હોય ત્યારે એક કોફીના કપનું તાપમાન $t$ મિનીટમાં $90^{\circ} \mathrm{C}$ થી ઘટીને $80^{\circ} \mathrm{C}$ થાય છે. આવા જ કોફીના કપનું તાપમાન ઓરડાનું તાપમાન $20^{\circ} \mathrm{C}$ જેટલું સમાન હોય ત્યારે $80^{\circ} \mathrm{C}$ થી ઘટીને $60^{\circ} \mathrm{C}$ થાય તે માટે લાગતો સમય $......$ છે.View Solution
- 9ધ્રુવ પ્રદેશમાં તળાવ પર $1 cm$ બરફનો સ્તર બનતા $7$ કલાક લાગે છે.તો બરફની જાડાઇ $1 cm$ થી $2 cm$ થતાં લાગતો સમય ?View Solution
- 10$ {r_1} $ અને $ {r_2} $ ત્રિજયા ધરાવતા સમાન દ્રવ્યના ગોળાના સપાટીના તાપમાન $ {T_1} $ અને $ {T_2} $ છે.જો તેનો ઉત્સર્જન પાવર સમાન હોય,તો ત્રિજયાનો ગુણોત્તર કેટલો થાય?View Solution
