એક આદર્શ વાયુ અલ્પ સ્થાયી $( quasi$ $static )$ પ્રત્યાવર્તી પ્રક્રિયામાંથી પસાર થાય છે.જેમાં તેનો મોલાર વિશિષ્ટ ઉષ્મા $C$ અચળ રહે છે.જો આ પ્રક્રિયા દરમિયાન દબાણ $P$ અને કદ $ V$ વચ્ચેનો સબંધ $PV^n$ = અચળ વડે આપવામાં આવે,તો $‘n’$ માટે ( અહીં $C_P$ અને $C_V$ ક્રમશ: અચળ દબાણે મોલર વિશિષ્ટ ઉષ્મા અને અચળ કદે મોલર વિશિષ્ટ ઉષ્મા છે.)
JEE MAIN 2016, Diffcult
d
For a polytropic process
For a polytropic process
\(C = {C_V} + \frac{R}{{1 - n}}\) \(\therefore C - {C_V} = \frac{R}{{1 - n}}\)
\(\therefore 1 - n = \frac{R}{{C - {C_V}}}\) \(\therefore 1 - \frac{R}{{C - {C_V}}} = n\)
\(\therefore n = \frac{{C - {C_V} - R}}{{C - {C_V}}} = \frac{{C - {C_V} - {C_P} + {C_V}}}{{C - {C_V}}}\)
\( = \frac{{C - {C_P}}}{{C - {C_V}}}\left( {{C_P} - {C_{V = R}}} \right)\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionઅચળ દબાણે અને અચળ કદે તાપમાનમાં એકમ ફેરફાર કરવાથી દ્વિ-પારિમાણ્કિ વાયુની આંતરિકઊર્જામા થતો ફેરફારનો ગુણોત્તર કેટલો થાય?
- 2પાત્ર $A$ અને $B$ માં $H_2$ અને $O_2$ સમાન તાપમાને ભરેલો છે.પાત્ર $B$ નું કદ $A$ કરતાં બમણું છે. ગતિઊર્જાનો ગુણોત્તર કેટલો થાય?View Solution
- 3View Solutionત્રિપરમાણ્વિક વાયુ માટે મુકતાતાના અંશો કેટલા હોય?
- 4આદર્શ વાયુ માટે અચળ તાપમાને દબાણ $P$ વિરુદ્ધ ઘનતા $\rho $ નો આલેખ કેવો મળશે?View Solution
- 5View Solutionનીચે પૈકી કયો આલેખ આદર્શ વાયુ જેવુ વલણ ધરાવે છે.
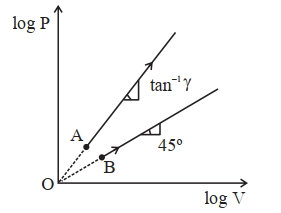
- 6આકૃતિમાં બે થમોડાયનેમિક પ્રક્રિયાઓ દર્શાવેલ છે. પ્રકિયા $\mathrm{A}$ અને $\mathrm{B}$ માટે મોલર ઉષ્મા ધારિતા $\mathrm{C}_{\mathrm{A}}$ અને $\mathrm{C}_{\mathrm{B}}$ છે. અચળ દબાણે અને અચળ કદે મોલર ઉષ્મા ધારિતા અનુકમે $\mathrm{C}_{\mathrm{P}}$ અને $\mathrm{C}_{\mathrm{V}}$ છે. સાચું વિધાન પસંદ કરો.View Solution
- 7કોઈ ચોકકસ તાપમાને પાત્રમાં ભરેલ ઓકિસજન અણુની $rms$ ઝડપ $\left(1+\frac{5}{x}\right)^{\frac{1}{2}}$ મળે છે; જ્યા $v$ એ અણુની સરેરાશ ઝડપ છે. $x$ નું મૂલ્ય ........ હશે. $\left(\pi=\frac{22}{7}\right)$View Solution
- 8નીચેનામાંથી કયો સાર્વત્રિક અચળાંક છે $?$View Solution
- 9$1\, kg$ દ્વિ-પરમાણુક વાયુ $8 \times 10^4 N/m^{2}$ ના દબાણે છે. વાયુની ઘનતા $4 kg/m^3$ છે. વાયુની ઉષ્મીય ગતિ સાથે સંકળાયેલ ઊર્જા કેટલી હશે ?View Solution
- 10નિશ્ચિત જથ્થાના વાયુનું અચળ દબાણે કદ $V$ છે. જો વાયુનું તાપમાન એટલું વધારવામાં આવે તો અણુના $v_{rms}$ નું મૂલ્ય બમણું થાય છે, તો તેનું નવું કદ .......View Solution
