કાર્ય ઊર્જા પ્રમેય અનુસાર પદાર્થ પર પરિણામી બળ વડે થતું કાર્ય, પદાર્થની ગતિ-ઊર્જાના ફેરફાર જેટલું હોય છે.
બુલેટની પ્રારંભિક ગતિઉર્જા \( = \frac{1}{2}m{\upsilon _0}^2\) વેગ અડધો થાય ત્યારે ગતિ ઉર્જા \( = \frac{1}{2}m{\left( {\frac{{{\upsilon _0}}}{2}} \right)^2}\,\, = \,\frac{1}{8}m{\upsilon _0}^2\)
કાર્ય ઉર્જા પ્રમેય અનુસાર \(,\,W = \frac{1}{8}m{\upsilon _0}^2\, - \frac{1}{2}m{\upsilon _0}^2\,\)
\(\,\therefore \,\,\,F\, \cdot \,d\, = \, - \frac{3}{8}m{\upsilon _0}^2\,\,\,\therefore \,\,\,\,F \times 6\, = \, - \frac{3}{8}m{\upsilon _0}^2\,\,\,\therefore \,\,\,F\, = \, - \frac{1}{{16}}m{\upsilon _0}^2\)
હવે, બુલેટ વઘારાનું \(1\) અંતર કાપી સ્થિર થાય છે. આ કિસ્સામાં બુલેટની પ્રારંભિક ગતિ-ઊર્જા \(= 1/2 mv_0^2,\) અંતિમ ગતિ-ઊર્જા \(= 0\)
કાર્ય ઉર્જા પ્રમેય અનુસાર \(,W = 0 - \frac{1}{8}m{\upsilon _0}^2\,\,\,\therefore \,\,\,\,F \cdot {d_1} = - \frac{1}{8}m{\upsilon _0}^2\,\,\)
\(F\) ની કિમત મુક્તા\(,\, - \frac{1}{{16}}m{\upsilon _0}^2 \times {d_1} = - \frac{1}{8}m{\upsilon _0}^2\,\,\,\,\therefore \,\,\,{d_1}\, = \,2\,cm\)
Download our appand get started for free
Similar Questions
- 1સમાન દળ ધરાવતી બે વસ્તુઓ $A$ અને $B$ એક પરિમાણમાં સંપૂણ અસ્થિસ્થાપક અથડામણ (સંધાત) અનુભવે છે. વસ્તુ $A, v_1$ વેગથી ગતિ કરે છે. જ્યારે વસ્તુ $B$ એ સંધાત પહેલા વીરામાવસ્થામાં છે. તંત્રનો સંધાત બાદ વેગ $v_2$ બને છે. $v_1: v_2$ ગુણોતર. . . . . . . થશે.View Solution
- 2બે $m$ દળના બ્લોક $A $ અને $B$ ને $L$ લંબાઇ અને $k$ બળઅચળાંક ધરાવતી સ્પિંગ્ર વડે જોડેલાં છે. $m$ દળ ધરાવતો $C$ બ્લોક $v$ વેગથી ગતિ કરીને $A$ સાથે અથડાતા સ્પિંગ્રનું મહત્તમ સંકોચન કેટલું થાય?View Solution
- 3$1\, m$ ઊંચાઈ ધરાવતા ટેબલ પર એક $1.9\, kg$ દળનો બ્લોક પડેલો છે. $0.1\, kg$ ધરાવતી ગોળી આ બ્લોક સાથે અથડાય અને તેની સાથે જોડાઈ જાય છે. જો અથડાતાં પહેલા આ ગોળીનો સમક્ષિતિજ દિશામાં વેગ $20\, m / s$ હોય તો પછી બ્લોક જ્યારે જમીન સાથે અથડાય તેની પહેલા આ જોડાયેલા તંત્રની ગતિઉર્જા કેટલા $J$ હશે?View Solution
$[g =10\, m / s ^{2}$. ધારો કે તેમાં કોઈ ચાક ગતિ નથી અને અથડામણ પછી ઉર્જાનો વ્યય નહિવત છે.$]$
- 4$1 \;kg $ દળવાળા પદાર્થને $20\; m/s$ જેટલા વેગથી ઊર્ધ્વ તરફ ફેંકવામાં આવે છે. પરિણામે તે $18\; m$ જેટલી ઊંચાઇ પ્રાપ્ત કર્યા બાદ ક્ષણ પૂરતો સ્થિર થાય છે. હવાના ઘર્ષણના કારણે ગુમાવતી ઊર્જા કેટલી ($J$ માં) હશે? ($g=10 \;ms^{-2}$)View Solution
- 5$ 2.05 \times {10^6}\;kg $ દળ ધરાવતી ટ્રેનનો વેગ $5\; min$ માં $ 5\;m/s $ થી $25\; m/s $ થાય છે,તો એન્જિનનો પાવર કેટલા ......... $MW$ હશે?View Solution
- 6$m$ દળના પદાર્થને $l$ લંબાઇની દોરી વડે લટકાવેલ છે.પદાર્થને સમક્ષિતિજ વેગ આપવાથી દોરી ${60^°}$ નો ખૂણો બનાવે છે.તો સમતોલન સ્થાન પાસે દોરીમાં તણાવ કેટલો હશે?View Solution
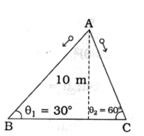
- 7આકૃતિમાં દર્શાવ્યા પ્રમાણે બે ગોળાઓને બિંદુ $A$ થી અનુક્રમે $AB$ તથા $AC$ પથ પર મુક્ત કરવામાં આવે છે, તો બંને ગોળાને ઢાળના તળિયે પહોંચવા માટે લાગતા સમય અનુક્રમે.......અને.......થાય. બંને સપાટીઓ લીસી ($g = 10 m/s^2$ લો.)View Solution
- 8$M$ દળવાળો કણ સ્થિર સ્થિતિમાંથી ગતિની શરૂઆત કરી અચળપ્રવેગી ગતિ કરે છે. જો $T$ સમયમાં કણે પ્રાપ્ત કરેલો વેગ $V$ હોય, તો કણને અપાયેલો પાવર કેટલો હશે?View Solution
- 9$h$ ઉંચાઈની એક ભેખડ પરથી એક ભારે (વજનદાર) પથ્થરને $v $ ઝડપે ફેંકવામાં આવે છે. પથ્થર જમીનને મહત્તમ ઝડપે અથડાય તે માટે તેને કેવી રીતે અને કઈ દિશામાં ફેંકવો જોઈએ?View Solution
- 10ઈલેકિટ્રક મોટર $40 N$ નું બળ તાર પર લગાડીને પદાર્થને $ 1 min$ માં $ 30 m $ ખસેડે છે.તો મોટરનો પાવર $Watts$ માં કેટલો થશે?View Solution
