એક ઇલેક્ટ્રોન અને પ્રોટોન એકબીજાથી ખુબ જ દૂર છે. ઇલેક્ટ્રોન પ્રોટોન તરફ $3\, {eV}$ ની ઉર્જાથી ગતિ કરવાનું શરૂ છે. પ્રોટોન ઇલેક્ટ્રોનને પકડે છે અને બીજી ઉત્તેજિત સ્થિતિમાં હાઇડ્રોજન પરમાણુની રચના કરે છે. આ પ્રક્રિયા દરમિયાન પરિણમતો ફોટોન $4000\, \mathring {{A}}$ થ્રેશોલ્ડ તરંગલંબાઇની પ્રકાશ ફોટોસંવેદી ધાતુ પર આપાત થાય છે. તો ઉત્સર્જીત ફોટોઇલેક્ટ્રોનની મહતમ ગતિઉર્જા કેટલા ${eV}$ હશે?
JEE MAIN 2021, Medium
Download our app for free and get started
c
Initially, energy of electron \(=+3 {eV}\)
Initially, energy of electron \(=+3 {eV}\)
Finally, in \(2^{\text {nd }}\) excited state,
\(E=-\frac{(13.6\, {eV})}{3^{2}}\)
\(=-1.51 \,{eV}\)
Loss in energy is emitted as photon,
So, photon energy \(\frac{{hc}}{\lambda}=4.51\, {eV}\)
No, photoelectric effect equation
\({KE}_{\max }=\frac{{hc}}{\lambda}-\phi=4.512-\left(\frac{{hc}}{\lambda_{{m}}}\right)\)
\(=4.51\, {eV}-\frac{12400\, {eV} \stackrel{\circ}{{A}}}{4000\, \stackrel{\circ}{{A}}}\)
\(=1.41\, {eV}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionઈલેકટ્રોનની ગતિઊર્જા બમણી કરતાં દ-બ્રોગ્લી તરંગલંબાઇ કેટલી થાય?
- 2એક કણ $E$ જેટલી ગતિઉર્જાથી ગતિ કરે છે જેની દ’બ્રોગલી તરંગલંબાઈ $\lambda$ છે. જો ઊર્જામાં $\Delta \mathrm{E}$ જેટલો વધારો કરવામાં આવે તો દ’બ્રોગલી તરંગલંબાઈ $\frac {\lambda}{2} $ થાય છે તો $\Delta \mathrm{E}$ કેટલું હશે?View Solution
- 3નીયે બે વિધાનો આપેલા છેઃ એકને કથન $A$ અને બીજાન કારણ $R$ થી દશાર્વેલ છે:View Solution
કથન $A$: પ્રકાશની આવૃત્તિના વધારા સાથે ફોટોનની સંખ્યા વધે છે.
કારણ $R$: આપાત વિકિરણની આવૃત્તિમાં વધારા સાથે ઉત્સર્જિત ઇલેકટ્રોનની મહત્તમ ગતિઊર્જા વધે છે.
ઉપરોક્ત વિધાનોનાં સંદર્ભમાં, નીચે આપેલા વિકલ્પોમાંથી સૌથી યોગ્ય ઉત્તર પસંદ કરોઃ
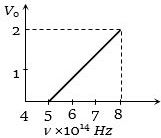
- 4ફોટોઇલેકટ્રોનનો સ્ટોપિંગ વોલ્ટેજ ${V_0}$ વિરુધ્ધ આપાત આવૃત્તિ $v$ નો આલેખ આપેલ છે.તો થ્રેશોલ્ડ તરંગલંબાઇ કેટલી થાય?View Solution
- 5આ પ્રશ્નના બે વિધાન છે : વિધાન $-1$ અને વિધાન $-2$. વિધાનોની નીચે આપેલાં ચાર વિક્પોમાંથી એવું એક વિકલ્પ પસંદ કરો કે જે આ બે વિધાનોને શ્રેષ્ઠ રીતે રજૂ કરતું હોય.View Solution
વિધાન $-1$ : ડેવીસન-ગર્મરના પ્રયોગે ઇલેક્ટ્રોનની તરંગ પ્રકૃતિ શોધી કાઢી.
વિધાન $-2$ : જો ઇલેક્ટ્રોન તરંગ પ્રકૃતિ ધરાવે તો તેમનું વ્યતિકરણ અને વિવર્તન થઈ શકે.
- 6ઇલેકટ્રોનની ગતિઊર્જા $log E$ અને દ-બ્રોગ્લી તરંગલંબાઇ $ log\lambda $ માટેનો આલેખ કેવો થાય?View Solution
- 7ધાતુનાં કાર્ય વિધેયથી બે ગણી અને દસ ગણી ઊર્જા ધરાવતી ફોટોનની બે ધારા (પ્રવાહો) અને વારાફરતી ધાતુ સપાટી પર આપાત કરવામાં આવે છે. બંન્ને કિસ્સામાં અનુક્રમે ઉત્સર્જાયેલા ફોટો ઈલેક્ટ્રોન્સના મહત્તમ વેગના ગુણોત્તરનાં મૂલ્યો $x: y$ છે. $x$ ના મૂલ્ય ...... છે.View Solution
- 8ધાતુની સપાટી પર એક $6\ eV$ ઊર્જા વાળો ફોટોન આપાત થાય છે. જેનું કાર્ય વિધેય $2\ eV$ છે. ઈલેક્ટ્રોનનું ઉત્સર્જન અટકાવવા માટે લાગુ પાડેલ ન્યૂનત્તમ રિવર્સ સ્થિતિમાન ........ $V$ છે.View Solution
- 9$66 eV$ ની ઊર્જા ધરાવતા ફોટોનની આવૃત્તિ કેટલી થાય?View Solution
- 10View Solutionસોડિયમ ધાતુની સપાટીમાંથી ઉત્સર્જાતા ફોટોઈલેકટ્રૉન માટે નીચેમાંથી કયું વિધાન સાચું છે.