એક કાલ્પનિક પ્રતિક્રિયા માટે $A \to B$, પુરોગામી અને પ્રતિગામી પ્રક્રિયાઓ માટે સક્રિયકરણ ઊર્જાઓ અનુક્રમે $19\, kJ/mole$ અને $ 9 \,kJ/mole$ છે,ત્યારે પ્રક્રિયા ની ઉષ્મા ....$kJ$ છે.
AIPMT 2000, Medium
Download our app for free and get started
c
(c)$\Delta H = {E_a}$ for forward reaction $ - {E_a}$ for backward reaction $ = 19 - 9 = 10\,kJ$.
(c)$\Delta H = {E_a}$ for forward reaction $ - {E_a}$ for backward reaction $ = 19 - 9 = 10\,kJ$.
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
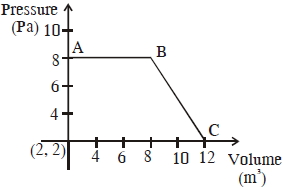
- 1એક આદર્શ વાયુ કે જે આકૃતિમાં દર્શાવેલા માર્ગ $ABC$ પર પ્રતિવર્તી વિસ્તરણ પામે છે તેના દ્વારા થતા કાર્યની માત્રા ............ થશે.View Solution
- 2નીચેનામાંથી કયું સમીકરણ $CH_4$ ની પ્રમાણીત નિર્માણ ઉષ્મા દર્શાવે છે ?View Solution
- 3$1\,mole$ આદર્શવાયુ ને પ્રતિવર્તીય અને સમોષ્મીય રીતે $27^{\circ}\,C$ તાપમાન થી વિસ્તરવા દેવામાં આવે છે. થયેલ કાર્ય $3\,kJ\,mol ^{-1}$ છે. વાયુનું અંતિમ તાપમાન $.........K$ છે. (નજીકનો પૂર્ણાંક) આપેલ : $CV _{ V }=20\,J\,mol ^{-1}\,K ^{-1}$View Solution
- 4View Solutionનીચેના પૈકી ક્યુ વિધાન સાચું છે ?
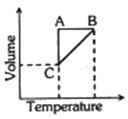
- 5કોઈ વાયુના પાંચ મોલને શ્રેણીમાં થતા ફેરફારના ઘટનાક્રમમાં મૂકવામાં આવેલ છે. જે નીચે આપેલા આલેખ વડે દર્શાવી શકાય છે, તો આ આલેખમાં $A$ $\rightarrow$ $B$, $B$ $\rightarrow$ $C$ અને $C$ $\rightarrow$ $A$ અનુક્રમે શું હશે ?View Solution
- 6આપેલView Solution
$C_{(graphite)} +O_2(g) \rightarrow CO_2(g)\,;$ $\Delta _rH^o=-395.5 \, kJ\,mol^{-1}$
$H_2 (g) + \frac{1}{2} O_2 (g) \rightarrow H_2O(l)\,;$ $\Delta _rH^o =-285.8\, kJ\, mol^{-1}$
$CO_2(g) + 2H_2O(l) \rightarrow CH_4(g) + 2O_2(g)\,;$ $\Delta _rH^o = + 890.3\, kJ\, mol^{-1}$
ઉપર દર્શાવેલ થર્મોરાસાયણિક સમીકરણોને આધારે $298\, K$ તાપમાને પ્રક્રિયા $C_{(graphite)} + 2H_2(g) \rightarrow CH_4(g) $
માટે $\Delta_{r} H^{\circ}$ ની કિંમત ........... $kJ \,mol^{-1}$
- 7અચળ તાપમાને અને દબાણે પ્રણાલી માટે ગીબ્સ ઉર્જાનો ફેરફાર ($\Delta G$ પ્રણાલી ) માટે સાચું વિધાન ઓળખો.View Solution
- 8$500\,mL$ $0.2\, N$ $H_2SO_4$ ને $50\, mL$ $1\,N$ $KOH$ સાથે મિશ્ર કરવામાં આવે ત્યારે કેટલી ઉષ્મા ઉત્પન્ન થશે ?View Solution
- 9નીચે બે વિધાનો આપેલા છે એકને કથન $A$ વડે લેબલ કરેલ છે અને બીજાને કારણ $R$ વડે લેબલ કરેલ છે.View Solution
કથન $A : \Delta_r G =- nFE _{\text {cell }}$ કોષ સમીકરણમા, $\Delta_{ r } G$ નું મૂલ્ય $n$ પર આધાર રાખે છે.
કારણ $R :E_{\text {cell }}$ કોષ એ વિશિષ્ટ ગુણધર્મ $(intensive\,property)$ છે અને $\Delta_{ r } G$ એ માત્રાત્મક ગુણધર્મ $(extensive\,property)$ છે.
ઉપરનાં વિધાનોના સંદર્ભમાં, નીચે આપેલા વિકલ્પોમાંથી સાચો જવાબ પસંદ કરો :
- 10આદર્શ વાયુના એક મોલ માટે, આમાંથી કયું વિધાન સાચું હોવું જોઈએ $?$View Solution
$(a)$ $U$ અને $H$ દરેક તાપમાન પર જ આધાર રાખે છે
$(b)$ દબનીયતા પરિબળ $z$ $1$ની બરાબર નથી
$(c)$ $C _{ P , m }- C _{ V , m }= R$
$(d)$ કોઈ પ્રક્રિયા માટે $d U = C _{ V } d T$