એક કાર સ્થિર સ્થિતિમાંથી ગતિ શરૂ કરીને પ્રથમ $S$ અંતર $f$ પ્રવેગથી કાપે છે, ત્યારબાદ $t$ સમય સુધી અચળ ઝડપે ગતિ કરે છે. ત્યારબાદ $\frac{f}{2}$ ના પ્રતિપ્રવેગથી ગતિ કરી સ્થિર થાય છે. જો કુલ અંતર $15S$ હોય, તો ....
AIEEE 2005, Diffcult
c
(c) Let car starts from point \(A\) from rest and moves up to point \(B\) with acceleration \(f\)
(c) Let car starts from point \(A\) from rest and moves up to point \(B\) with acceleration \(f\)
Velocity of car at point \(B\), \(v = \sqrt {2fS} \)
\(As \,{v^2} = {u^2} + 2as]\)
Car moves distance \(BC\) with this constant velocity in time \(t\)
\(x = \sqrt {2fS} \,.\,t\) ......(i) [As \(s = ut\)]
So the velocity of car at point \(C\) also will be \(\sqrt {2fs} \) and finally car stops after covering distance y.
Distance \(CD ⇒y = \frac{{{{(\sqrt {2fS} )}^2}}}{{2(f/2)}}\)\( = \frac{{2fS}}{f} = 2S\)....(ii) \([{\rm{As }}{v^{\rm{2}}} = {u^2} - 2as\, \Rightarrow \,s = {u^2}/2a]\)
So, the total distance \(AD\) = \(AB + BC + CD=15S\) (given)
\(⇒\) \(S + x + 2S = 15S\) \(⇒ x = 12S\)
Substituting the value of x in equation (i) we get
\(x = \sqrt {2fS} \,.\,t ⇒ 12S = \sqrt {2fS} .t ⇒ 144{S^2} = 2fS.{t^2}\)
\(⇒\) \(S = \frac{1}{{72}}f{t^2}\).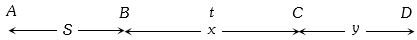
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1${m_a}$ અને ${m_b}$ દળ ધરાવતા બે પદાર્થને અલગ અલગ ઊંચાઈ $a$ અને $b$ પરથી મુક્ત કરવામાં આવે છે. તો બંને પદાર્થ દ્વારા આ અંતર કાપવા માટે લાગતાં સમયનો ગુણોત્તર કેટલો થાય?View Solution
- 2એક પદાર્થ પ્રથમ $5\, sec$ માં $40 \,m$ અને પછીની $5\, sec$ માં $65 \,m$ અંતર કાપે છે,તો પદાર્થનો શરૂઆતનો વેગ કેટલા........$m/s$ હોવો જોઈએ?View Solution
- 3જો એક પથ્થરને જમીન પરથી પ્રક્ષિપ્ત કરવામાં આવે તો તે તેના ગતિપથના સર્વોચ્ય બિંદુ પર પહોયતા $4 \,s$ જેટલો સમય લે છે, તો તેના ઉડ્ડયનનો સમય ............. $s$ હશે?View Solution
- 4View Solutionએક સ્ટીલ ના બોલ ને ઊંચાઇથી આરસ પર ફેકવામાં આવે તો વેગ વિરૂઘ સમય નો ગ્રાફ કેવો મળે?
- 5$h$ ઊંચાઇ પર $u$ વેગથી એક પ્લેન સમક્ષિતિજ દિશામાં ગતિ કરે છે.તેમાંથી પથ્થરને મુકત કરતાં જમીન પર પહોચે ત્યારે તેનો વેગ કેટલો હશે?View Solution
- 6એક બોલને $u$ વેગ સાથે શિરોલંબ ઊર્ધ્વ દિશામાં ઊછાળવામાં આવે છે, ઉપરની ગતિની છેલ્લી $t$ સેકન્ડમાં બોલે કાપેલું અંતર કેટલું હશે?View Solution
- 7$x$ - અક્ષની સાપેક્ષે ગતિ કરી રહેલા કણોનો વેગ $(v)$ તેના સ્થાન $x$ સાથે આકૃતિમાં દર્શાવ્યા મુજબ બદલાય છે. કણનો પ્રવેગ $(a)$ એ સ્થાન $(x)$ સાથે શેના તરીકે બદલાય છે ?View Solution
- 8એક કણને $H$ ઊંચાઇના બહુમાળી મકાન પરથી ઊર્ધ્વ દિશામાં $u $ જેટલી ઝડપે ફેંકવામાં આવે છે. કણને જમીન પર પહોંચતા લાગતો સમય તેની મહત્તમ ઊંચાઇએ પહોંચતા લાગતો સમય કરતાં $n$ ગણો છે. $H,u$ અને $n$ વચ્ચેનો સંબંધ શું થાય?View Solution
- 9એ કે કાર સુરેખ રેખા પર ગતિ કરે છે. જેમકે આકૃતિમાં $OP$. આ કાર $18\; s$ માં $O$ થી $P$ જાય છે અને $6\; s$ માં $P$ થી $Q$ પરત જાય છે. કાર $O$ થી $P$ જાય ત્યારે તેનો સરેરાશ વેગ અને સરેરાશ ઝડપ શું હશે ?View Solution

- 10કોઈપણ તત્કાલ પર, સીધી રેખા સાથે ગતિ કરતાં કણોનો વેગ અને પ્રવેગ $v$ અને $a$ છે. નીચેનામાંથી શું હોવાના કારણે કણોની ઝડપ વધી રહી છે.View Solution
