એક કણ $xy$ સમતલમાં વેગ પર આધારિત બળ $\overrightarrow{ F }= k \left( v _{ y } \hat{ i }+ v _{ x } \hat{ j }\right)$ દ્વારા ગતિ કરે છે, જ્યાં $v _{ x }$ અને $v _{ y }$ એ વેગ $\overrightarrow{ v } $ ના $x$ અને $y$ દિશાના ઘટકો છે. જો $\overrightarrow{ a }$ કણનો વેગ હોય તો કણ માટે નીચે પૈકી કયા વિધાનો સત્ય હશે?
JEE MAIN 2020, Diffcult
c
\(\frac{ dv _{ x }}{ dt }=\frac{ k }{ m } v _{ y }\)
\(\frac{ dv _{ x }}{ dt }=\frac{ k }{ m } v _{ y }\)
\(\frac{ dv _{ y }}{ dt }=\frac{ k }{ m } v _{ x }\)
\(\frac{ d v_{ y }}{ dv _{ x }}=\frac{ v _{ x }}{ v _{ y }} \Rightarrow \int v _{ y } dv _{ y }=\int v _{ x } dv _{ x }\)
\(v_{y}^{2}=v_{x}^{2}+C\)
\(v _{ y }^{2}- v _{ x }^{2}= constant\)
Option \((3)\)
\(\overrightarrow{ v } \times \overrightarrow{ a }=\left( v _{ x } \hat{ i }+ v _{ y } \hat{ j }\right) \times \frac{ k }{ m }\left( v _{ y } \hat{ i }+ v _{ x } \hat{ j }\right)\)
\(=\left( v _{ x }^{2} \hat{ k }- v _{ y }^{2} \hat{ k }\right) \frac{ k }{ m }\)
\(=\left(v_{x}^{2}-v_{y}^{2}\right) \frac{k}{m} \hat{k}\)
\(=\) \(Constant\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1સમય $x$ ના વિધેય તરીકે સમક્ષિતિજ લીસી સપાટી પર $1 \;kg $ દળનો પદાર્થનું સ્થાનાંતર $x = \frac{{{t^3}}}{3}$ સૂત્ર વડેે આપવામાં આવે છે. પ્રથમ એક સેકન્ડ માટે બાહ્ય પરિબળ વડે થતું કાર્ય ........... $J$ છે.View Solution
- 2પંપનો ઉપયોગ પાઈપમાં અમુક દરથી પાણી મોકલવા માટે થાય છે. પાઈપમાંથી $n$ ગણું પાણી સમાન સમયગાળામાં મેળવવા માટે પાણીનો વેગ, પાણીનું બળ અને પંપનો પાવર કેટલો વધારવો જોઈએ?View Solution
- 3બે અવલોકનકારો $v$ ઝડપે અને એકબીજાની સાપેક્ષે સુરેખરેખા પર ગતિ કરે છે તેમ લો તેઓ $m $ દળનો એક ટુકડો $l$ અંતર સુધી ખરબચડી સપાટી પર ગતિ કરે છે તેનું અવલોકન કરે છે. બે અવલોકનકાર દ્વારા કરેલા અવલોકનમાં નીચે આપેલ પૈકી કઈ રાશિ સમાન રહેશે?View Solution
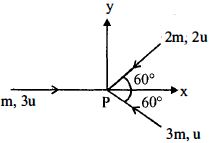
- 4આકૃતિ માં બતાવ્યા મુજબ ત્રણ દળો $m,\,2\,m$ અને $3\,m$ $x-y$સમતલ માં અનુક્રમે $3\,u,\,2\,u\,$ અને $u$ ઝડપથી ગતિ કરે છે. ત્રણેય દળો એકજ બિંદુ $P$ એ સંઘાત પામે છે અને એકબીજા સાથે ચોંટી જાય છે. તો પરિણામી દળ નો વેગ કેટલો હશે?View Solution
- 5વિધાન: $m$ દળના નાના $n$ દડાઓ $u$ વેગથી દર સેકંડે સપાટી સાથે સ્થિતિસ્થાપક સંઘાત રચે છે. સપાટી દ્વારા અનુભવાતું બળ $2\,mnu$ હશે.View Solution
કારણ: સ્થિતિસ્થાપક સંઘાત બાદ દડો તેટલા જ વેગ થી ઉછળે છે.
- 6View Solutionજ્યારે બે કણો અથડાય છે ત્યારે સામાન્ય રીતે શું સાચું હશે?
- 7અચળ પાવરના એક ઉદગમની અચર નીચે એક પદાર્થ એક દિશામાં ગતિ કરવાનું શરૂ કરે છે. આપેલ આલેખોમાંથી કયો આલેખ સ્થાનાંતર $(s)$ નું સમય $(t)$ સાથેનો બદલાવ સારી રીતે રજૂ કરે છે ?View Solution
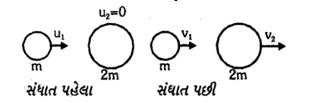
- 8એક બોલ સ્થિર સ્થિતિએ રહેલા તેના કરતા બમણું દળ ધરાવતા બોલ સાથે $1.5 m/s $ ના વેગથી હેેડઓન સંઘાત કરે છે. જો રેસ્ટીટ્યૂશન ગુણાંક $0.6$ હોય તો અથડામણ પછી તેઓનો વેગ કેટલો હશે ?View Solution
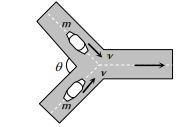
- 9View Solutionસમાન દળ અને સમાન વેગથી જતી બે કાર વચ્ચે સંપૂર્ણ અસ્થિતિસ્થાપક અથડામણ થતાં બંને કારનો વેગ
- 10$x$ અક્ષની દિશામાં મુક્ત રીતે ગતિ કરતા $1 kg $ દળના કણની સ્થિતિ ઊર્જા $V(x)\,\, = \,\,\left( {\frac{{{x^4}}}{4}\, - \,\,\frac{{{x^2}}}{2}} \right)\,J$સૂત્રથી આપી શકાય કણની કુલ યાંત્રિક ઊર્જા $2 J $ છે. તો કણની મહત્તમ ઝડપથી $ (m/s)$ માં કેટલી હશે ?View Solution
