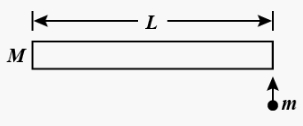
એક $l$ લંબાઇની અને $M$ દળની લાકડી એક ઘર્ષણરહિત સમક્ષિતિજ સપાટી પર પડેલ છે. $v$ વેગથી ગતિ કરતો એક $ m$ દળનો દડો આકૃતિમાં દર્શાવ્યામુજબ સ્થિતિસ્થાપક સંઘાત અનુભવે છે. સંઘાત પછી દડો સ્થિર થાય તો તેનું દળ કેટલું હશે ?
Diffcult
Download our app for free and get started
d
Applying the law of conservation of momentum
Applying the law of conservation of momentum
\(m v=M V \quad \ldots(1)\)
By conservation of angular momentum
\(m v(L / 2)=\left(\frac{M L^{2}}{12}\right) \omega \quad \ldots(2)\)
As the collision is elastic, we have
\(\frac{1}{2} m v^{2}=\frac{1}{2} M V^{2}+\frac{1}{2} I \omega^{3}\) \(...(3)\)
Substituting the values, we get \(m=M / 4\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionજ્યાર કોઈ તંત્ર પર લગાડવામાં આવતો ટોર્ક શૂન્ય હોય તો નીચેના માંથી શું અચળ હશે ?
- 2નકકર ગોળો વ્યાસને અનુલક્ષીને ફરે છે. તાપમાન વઘવાથી તેના કદમાં $1\%$ નો વઘારો થાય છે. તો કોણીય ઝડપView Solution
- 3$2\,m$ લંબાઈ અને $A$ જેટલું આડછેદનું ક્ષેત્રફળ અને $d$ ઘનતા ધરાવતો એક પાટલો નિયમિત સળીયો,તેની લંબાઈ ને લંબરુપે કેન્દ્ર માંથી પસાર થતી અક્ષને અનુલક્ષીને $\omega$ જેટલા કોણીય વેગથી ભ્રમણ કરે છે. ચાક્ગતિ ઊર્જાના સ્વરૂપમાં $\omega$ નું મૂલ્ય $\sqrt{\frac{\alpha E }{ Ad }}$ છે. $\alpha$ નું મૂલ્ય $...............$ હશે.View Solution
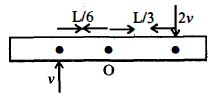
- 4લંબાઈ $L$ અને દળ $8\,m$ ની એક નિયમિત પાતળી પટ્ટી ને લીસ્સા સમક્ષિતિજ ટેબલ પર મૂકેલી છે. બે સૂક્ષ્મ દળો $m$ અને $2\,m$ સમાન સમક્ષિતિજ સમતલ માં પટ્ટીની પરસ્પર વિરુદ્ધ બાજુઓ તરફ અનુક્રમે $2v$ અને $v$ વેગથી ગતિ કરે છે. તે દળો પટ્ટી સાથેના સંઘાત બાદ પટ્ટીના કેન્દ્રથી અનુક્રમે $\frac{L}{3}$ અને $\frac{L}{6}$ અંતરે પટ્ટી પર ચોંટી જાય છે. પટ્ટી સંઘાતના પરિણામના ભાગરૂપે તેના દ્રવ્યમાન કેન્દ્રને અનુલક્ષીને ભ્રમણ શરૂ કરે છે તો પટ્ટીનો કોણીય વેગ કેટલો હશે?View Solution
- 5એક હળવી દોરીને $5\,kg$ દળ અને $70\,cm$ ત્રિજ્યા ધરાવતા એક પોલા નળાકારની આસપાસ વીટાળવામાં આવે છે. દોરીને $52.5\,N$ બળ વડે ખેંચવામાં આવે છે. નળાકારનો કોણીય પ્રવેગ .......... $rad\,s ^{-2}$ હશે.View Solution
- 6$h$ ઊંચાઇના ઢાળ પરથી ઘન નળાકાર મૂકતાં ચાકગતિઉર્જા અને કુલઉર્જાનો ગુણોત્તરView Solution
- 7$2\ kg $ દળ ધરાવતો પદાર્થ એ $2\ m$ ત્રિજ્યા ધરાવતા વર્તૂળમાર્ગ પર નિયમિત ગતિ કરે છે. જો તેના પર લાગતું કેન્દ્રગામી બળ $100\ N$ હોય, તો તેનું કોણીય વેગમાન ....... $J s $ થાય.View Solution
- 8$m$ દળ ધરાવતા કણને સમક્ષિતિજ સાથે $30^{\circ}$ ના કોણે $'u'$ જેટલા વેગથી પ્રક્ષિપ્ત કરવામાં આવે છે. જ્યારે કણ તેની મહત્તમ ઉંચાઈ $h$ એ હોય ત્યારે પ્રક્ષિમ બિંદુને અનુરૂપ (ફરતે) પ્રક્ષિપ્ત-કણના કોણીય વેગમાનનું મૂલ્ય_________છે.View Solution
- 9$1.6\ m $ પહોળા દરવાજાને ખોલવા માટે તેની ખુલ્લી બાજુની ધાર ઉપર $ 1\ N $ બળ ળગાડવું પડે છે. જો આ દરવાજાને મજાગરાથી એટલે કે તેની ભ્રમણાક્ષથી $ 0.4\ m$ દૂર આવેલા બિંદુ ઉપર બળ આપીને ખોલવો હોય, તો ...... $N$ બળ આપવું પડે .View Solution
- 10$2L $ લંબાઈનો સમાન સળીયાનો એક છેડો સમક્ષીતિજ સાથે સંપર્કમાં છે તથા બીજા છેડાને સમક્ષીતીજ સાથે $\alpha$ કોણ બનાવીને સંપર્ક આગળ સરકે નહીં તે રીતે છોડવામાં આવે તો સમક્ષીતિજ આવે ત્યારે તેનો કોણીય વેગ કેટલો હશે ?View Solution