\(M.I\) of complete disc about its center \(O.\)
\({l_{Total}} = \frac{1}{2}M{R^2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,....\left( i \right)\)
Mass of circular hole (removed)
\( = \frac{M}{4}\left( {As\,M = \pi {R^2}t\therefore M \propto {R^2}} \right)\)
\(M.I.\) of removed hole about its own ax is
\( = \frac{1}{2}\left( {\frac{M}{4}} \right){\left( {\frac{R}{2}} \right)^2} = \frac{1}{{32}}M{R^2}\)
\(M.I.\) of removed hole about \(O'\)
\(\begin{array}{l}
{I_{removed\,hole}} = {I_{cm}} + m{x^2}\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{M{R^2}}}{{32}} + \frac{M}{4}{\left( {\frac{R}{2}} \right)^2}\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{M{R^2}}}{{32}} + \frac{{M{R^2}}}{{16}} = \frac{{3M{R^2}}}{{32}}
\end{array}\)
\(M.I.\) of complete disc can also be written as
\(\begin{array}{l}
{I_{Total}} = {I_{removed\,hole}} + {I_{re\min ing\,disc}}\\
{I_{Total}} = \frac{{3M{R^2}}}{{32}} + {I_{remaining\,disc}}\,\,\,\,\,\,\,\,\,\,\,...\left( {ii} \right)
\end{array}\)
Form eq. \((i)\) and \((ii)\),
\(\begin{array}{l}
\frac{1}{2}M{R^2} = \frac{{3M{R^2}}}{{32}} + {I_{remaining\,disc}}\\
\Rightarrow {I_{remaining\,disc}}\\
\,\,\,\,\,\,\,\,\, = \frac{{M{R^2}}}{2} + \frac{{3M{R^2}}}{{32}} = \left( {\frac{{13}}{{32}}} \right)M{R^2}
\end{array}\)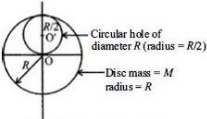
Download our appand get started for free
Similar Questions
- 1View Solutionકણ નિયમિત વર્તૂળાકાર ગતિ કરે છે. વર્તૂળના સમતલના કયાં બિંદુએ કણનું કોણીય વેગમાનનું સંરક્ષણ થશે ?
- 2એક $M$ દળ અને $R$ ત્રિજયાની પાતળી વર્તુળાકાર પ્લેટની ઘનતા $p\left( r \right) = {p_0}\,r$ મુજબ બદલાય છે જ્યાં $P_0$ અચળાંક અને $r$ કેન્દ્રથી અંતર છે.વર્તુળાકાર પ્લેટને લંબ અને તેની ધારમાથી પસાર થતી અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા $I = aMR^2$ હોય તો $a$ કેટલું થાય?View Solution
- 3બળ $\overrightarrow F = - 3\hat i + \hat j + 5\hat k$ દ્વારા બિંદુ $\overrightarrow r = 7\hat i + 3\hat j + \hat k$ પર લાગેલ ટોર્ક કેટલું હશે?View Solution
- 4નીચે બે વિધાનો આપેલ છે: એકને વિધાન $(A)$ તરીકે લેબલ થયેલ છે અને બીજું કારણ $(R)$ તરીકે લેબલ કરેલ છે,View Solution
વિધાન $(A)$ : જ્યારે ફટાકડો (રોકેટ) આકાશમાં વચ્ચે વિસ્ફોટ થાય છે, ત્યારે તેના ટુકડાઓ એવી રીતે ઉડે છે કે તે તેજ માર્ગ પર આગળ વધે છે, જે ફટાકડો જ્યારે વિસ્ફોટ ન પામ્યો હોય, તે માર્ગે આગળ વધતો હતો.
કારણ $(R)$: ફટાકડા (રોકેટ) નો વિસ્ફોટ ફક્ત આંતરિક બળોને કારણે થાય છે અને આ વિસ્ફોટ માટે કોઈ બાહ્ય બળ લાગતું નથી.
ઉપરોક્ત વિધાનોના સંદર્ભમાં, નીચે આપેલા વિકલ્પોમાંથી સૌથી યોગ્ય જવાબ પસંદ કરો.
- 5View Solutionગુરૂત્વાકર્ષકની અસર હેઠળ શિરોલંબ રીતે અધોદિશામાં પડતો પદાર્થ બે અસમાન દળોનાં ટુકડાંઓમાં વિભાજિત થાય છે. બંને ટુકડાઓનું એક સાથે લેવામાં આવેલું દ્રવ્યમાન કેન્દ્ર શું થાય?
- 6એક ચક્રની જડત્વની ચાકમાત્રા $4\ kg - {m^2}$ અને ગતિઉર્જા $200\ J$ છે.તેના પર $5\ N-m$ નું ટોર્ક લગાવાથી તે સ્થિર થાય,ત્યાં સુધીમાં કરેલા પરિભ્રમણ .......... $rev$View Solution
- 7View Solutionજો એક બોમ્બ ને સમક્ષિતિજ સાથે થોડાક ખૂણે ફેકવામાં આવે છે અને બોમ્બ ફુટયા પછી તેના ટુકડા અલગ અલગ દિશામાં પડતાં હોય તો દ્રવ્યમાનકેન્દ્ર ....
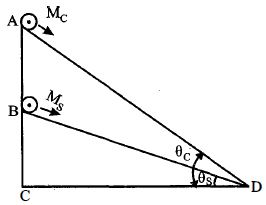
- 8આકૃતિમાં $M_c$ દળનું નળાકાર અને $M_s$ દળના ગોળાને અનુક્રમે બે ઢોળાવના બિંદુઓ $A$ અને $B$ પર મૂકેલા છે. જો તેઓ ઢોળાવ પર સરક્યાં વગર સમાન પ્રવેગથી ગતિ કરતાં હોય તો $\frac{{\sin \,{\theta _c}}}{{\sin \,{\theta _s}}}$ નો ગુણોત્તર કેટલો થાય?View Solution
- 9$12 \mathrm{~kg}$ ના એક ભારે લોખંડનાં સળિયાનો એક છેડો જમીન ઉપર અને બીજો છેડો એક માણસના ખભા ઉપર રહેલ છે. સળિયો સમક્ષિતિજ સાથે $60^{\circ}$ નો કોણ બનાવે છે, માણસ દ્વારા અનુભવાતું વજન______હશે.View Solution
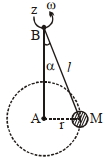
- 10$M$ દળના ગોળાને દળરહિત $l$ લંબાઈના સળિયા સાથે જોડીને આકૃતિમાં દર્શાવ્યા પ્રમાણે $\omega$ જેટલી કોણીય ઝડપથી ભ્રમણ કરાવવામાં આવે છે. બિંદુ $A$ ને અનુલક્ષીને $M$ નું કોણીય વેગમાન $L _{ A }$કે જે ધન $z$ અક્ષની દિશામાં છે. બિંદુ $B$ ને અનુલક્ષીને $M$ નું કોણીય વેગમાન $L _{ B }$ હોય તો નીચેનામાંથી કયું વિધાન સાચું પડે?View Solution