એક માપપટ્ટીથી એક નળાકારનો વ્યાસ અને ઊંચાઈ માપતા તે અનુક્રમે $12.6 \pm 0.1\, cm$ અને $34.2 \pm 0.1\, cm$ મળે છે. તેને અનુરૂપ સાર્થક અંકોમાં તેનું કદ કેટલું હશે?
JEE MAIN 2019, Medium
b
\(\begin{array}{l}
V = \pi {R^2}h = \frac{\pi }{4}{D^2}h\\
\,\,\,\,\,\,\, = 4260\,c{m^2}\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{{\Delta V}}{V} = 2\frac{{\Delta D}}{D} + \frac{{\Delta h}}{h}\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \left( {2 \times \frac{{0.1}}{{12.6}} + \frac{{0.1}}{{34.2}}} \right)V\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{2 \times 426}}{{12.6}} + \frac{{426}}{{34.2}}\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 67.61 + 12.459 = 80.075\\
\therefore \,\,\,\,\,\,\,\,\,\,\,\,\,\,V = 4260 \pm 80\,c{m^3}
\end{array}\)
\(\begin{array}{l}
V = \pi {R^2}h = \frac{\pi }{4}{D^2}h\\
\,\,\,\,\,\,\, = 4260\,c{m^2}\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{{\Delta V}}{V} = 2\frac{{\Delta D}}{D} + \frac{{\Delta h}}{h}\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \left( {2 \times \frac{{0.1}}{{12.6}} + \frac{{0.1}}{{34.2}}} \right)V\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{2 \times 426}}{{12.6}} + \frac{{426}}{{34.2}}\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 67.61 + 12.459 = 80.075\\
\therefore \,\,\,\,\,\,\,\,\,\,\,\,\,\,V = 4260 \pm 80\,c{m^3}
\end{array}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1અવરોધ $R$ અને સમય $T$ ના સ્વરૂપમાં, પરમીએબીલિટી $\mu $ અને પરમિટિવિટી $\varepsilon $ ના ગુણોત્તર $\frac{\mu } {\varepsilon}$ નું પરિમાણ શું થશે?View Solution
- 2View Solutionન્યુક્લિયસમાં રહેલા ન્યુક્લિઓનની બંધન ઉર્જા કયા ક્રમની હોય છે?
- 3અવરોધનું મૂલ્ય $10.845\ ohms$ અને પ્રવાહ $3.23\ amperes$ છે,અને તેનો વોલ્ટેજ $35.02935\ volts$ થાય છે.તો ........ $V$View Solution
- 4View Solutionદઢતા ગુણાંકનું (shear modulus) પારિમાણિક સૂત્ર શું થાય?
- 5વિદ્યાર્થી $A$ અને વિદ્યાર્થી $B$ સમાન પીચ ધરાવતા અને $100$ વર્તુળાકાર કાંપા ધરાવતા બે સ્ક્રૂગેજોનો ઉપયોગ આપેલ તારની ત્રિજ્યા માપવા માટે કરે છે. તારની ત્રિજ્યાનું સાચું મૂલ્ય $0.322\, {cm}$ છે. વિદ્યાર્થી $A$ અને $B$ દ્વારા વર્તુળાકાર સ્કેલના અવલોકનના તફાવતનું નિરપેક્ષ મૂલ્ય કેટલું હશે?View Solution
[જ્યારે સ્ક્રુ ગેજ બંધ હોય ત્યારે આકૃતિ $O$ સંદર્ભની સ્થિતિ દર્શાવે છે]
આપેલ : પીચ $=0.1 \,{cm}$.
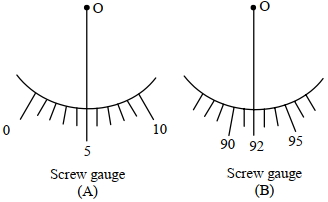
- 6$ {G^x}{c^y}{h^z} $ નું પારિમાણીક સૂત્ર લંબાઇ જેવું છે.જયાં $G,c$ અને $h$ ગુરુત્વાકર્ષણ અચળાંક, પ્રકાશનો વેગ અને પ્લાન્કનો અચળાંક છે. તો નીચેનામાથી $x,y$ અને $z$ ના કયા મૂલ્યો સાચા છે.View Solution
- 7વર્નિયર કેલીપર્સ માટે વર્નિયર અચળાંક $0.1 \,mm$ છે અને તેને $(-0.05) \,cm$. ની શૂન્ય ત્રુટિ છે. એક ગોળાનો વ્યાસ માપવામાં, મુખ્ય સ્કેલનું અવલોકન $1.7 \,cm$ વર્નિયરના $5$ માં કાપા સાથે સંપાત થાય છે. સાયો કરેલો વ્યાસ ............. $\times 10^{-2} \,cm$. હશે.View Solution
- 8ધારો કે $[{\varepsilon _0}]$ એ શૂન્યાવકાશની પરમિટિવિટી અને $[{\mu _0}]$ એ શૂન્યાવકાશ ની પરમીએબીલીટી દર્શાવે છે. જો $M =$ દળ , $L =$ લંબાઈ , $T =$ સમય અને $I =$ વિદ્યુતપ્રવાહ, તો ....View Solution
- 9એક સાર્વજનિક ચોરસ બાગ, $(100 \pm 0.2)\; m ^2$ નું ક્ષેત્રફળ ધરાવે છે. બાગની બાજુની લંબાઈ કેટલી હશે?View Solution
- 10$\frac{L}{RCV}$ નું પારિમાણિક સૂત્ર શું થાય?View Solution
