એક પૈડું તેની ભૌમિતિક અક્ષને અનુલક્ષીને $ 60\ rpm$ ની ઝડપથી ભ્રમણ કરે છે. જો આ અક્ષને અનુલક્ષીને પૈડાની જડત્વની ચાકમાત્રા $2\ kg m^2$ હોય,તો તેના ઉપયુક્ત ભ્રમણને એક મિનિટમાં રોકવા કેટલું ટોર્ક જોઇએ ?
Medium
Download our app for free and get started
c
\(\omega = 60\,rpm = \frac{{60 \times 2\pi }}{{60}} = 2\pi rad\,{s^{ - 1}}\)
\(\omega = 60\,rpm = \frac{{60 \times 2\pi }}{{60}} = 2\pi rad\,{s^{ - 1}}\)
\(;\,\,\,\,I = 2\,kg{m^2}\,,\,\,t = 60\,s,\,\,\,\,\tau = (?)\,\,\)
\(\tau = I\alpha = I.\left( {\frac{{0 - 2\pi }}{t}} \right) = \frac{{ - 2 \times 2\pi }}{{60}} = - \frac{\pi }{{15}}\,Nm\)
મૂલ્ય \( = \frac{\pi }{{15}}\,Nm\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
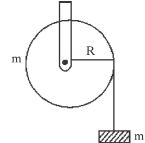
- 1$m $ દળ ધરાવતા પદાર્થને વજનરહિત દોરી વડે $m$ દળ અને $R$ ત્રિજયા ધરાવતા સમાંગી પોલા નળાકાર પર લટકાવવામાં આવે છે.જો દોરી નળાકાર પર સરકે નહિ તો તે સ્થિતિમાં આપેલ પદાર્થ કેટલા ગુરુત્વપ્રવેગથી નીચે પડશે?View Solution
- 2$R$ ત્રિજ્યા અને $L$ લંબાઈના નિયમિત ધનનળાકારની અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા $I _1$ છે. આ નળાકારમાંથી $R^{\prime}=\frac{R}{2}$ ત્રિજ્યા અને $L^{\prime}=\frac{L}{2}$ લંબાઈનો સમકેન્દ્રિય નળાકાર બનાવવામાં આવે છે. જો આ બનાવેલ નળાકારના ભાગની જડત્વની ચાકમાત્રા $I _2$ હોય, તો $\frac{I_1}{I_2}=...........$ (બંને $I _1$ અને $I _2$ નળાકારની અક્ષને અનુલક્ષીને છે)View Solution
- 3બિંદુ $ ( 2,-2,-2 )$ ને અનુલક્ષીને બિંદુ $( 2,0,-3 ) $ પર બળ $\overrightarrow {\;F} = 4\hat i + 5\hat j - 6\hat k$ ની ચાકમાત્રા આપવામાં આવે છે.View Solution
- 4$1.5\ m$ ત્રિજ્યાનું વ્હીલ $10\ rad/s^2$ ના અચળ પ્રવેગથી ચાકગતિ કરે છે તેની પ્રારંભિક કોણીય ઝડપ $\left( {\frac{{60}}{\pi }} \right)\,\,rpm.$ છે તેની કોણીય ઝડપ અને કોણીય સ્થાનાંતર $ t = 2.0\ sec$ એ ........ $rad$ થશે ?View Solution
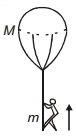
- 5એક $m$ દળના વ્યક્તિને $M$ દળના ફુગ્ગા સાથે દોરડું પકડીને હવામાં લટકાવવામાં આવે છે. જેમ જેમ તે વ્યક્તિ દોરડા પર ઉંચેે ચઢે છે, ફુગ્ગો ........View Solution
- 6સમાન દળ અને ત્રિજ્યા ધરાવતાં ચાર વસ્તુઓની જડત્વની ચાકમાત્રા $(M.I.)$ નીચે મુજબ દર્શાવાય છે.View Solution
$I _{1}=$ પાતળી રિંગની તેના વ્યાસને અનુલક્ષીને $M.I.,$
$I _{2}=$ વર્તુળાકાર તકતીની તેના કેન્દ્રમાંથી પસાર થતી અને તકતીને લંબ અક્ષને અનુલક્ષીને $M.I.$
$I_{3}=$ ઘન નળાકારની તેની અક્ષને અનુલક્ષીને $M.I.$ અને
$I _{4}=$ ઘન ગોળાની તેના વ્યાસને અનુલક્ષીને $M.I.$
તો :
- 7લંબાઈ $L$ ની એક પાતળી પટ્ટી માટે એકમ લંબાઈ દીઠ દળ $\lambda $ માં એક છેડા તરફથી અંતર વધતાં રેખીય વધારો થાય છે. જો તેનું કુલ દળ $M$ અને હળવા છેડે એકમ લંબાઈ દીઠ દળ $\lambda_0$ હોય તો હળવા છેડે થી દ્રવ્યમાન કેન્દ્રનું અંતર કેટલું હશે?View Solution
- 8એક પાતળી ચોરસ તકતી જેનું દળ $m$ અને બાજુની લંબાઈ $a$ છે તેના વિકર્ણને અનુલક્ષીને જડત્વની ચાકમાત્રા $I$ હોય તો ...View Solution
- 9$r $ ત્રિજ્યાવાળા સમાન પ્રકારના ત્રણ દડાઓ એકબીજાને અડે તેમ સમક્ષિતિજ સપાટી પર મૂકેલા છે. આ દડા એવી રીતે ગોઠવેલા છે, જેથી તેમના દ્રવ્યમાન-કેન્દ્રને જોડતા તેઓ સમબાજુ ત્રિકોણ બનાવે. આ તંત્રનું દ્રવ્યમાન-કેન્દ્ર ........ હશે.View Solution
- 10View Solutionઅચળ કોણીય ઝડપથી ગતિ કરતું પૈડુ ગતિ દરમિયાન બ્રેકનો અનુભવે કરે તો તેની ચક્રાવર્તનની ત્રિજ્યા =…..