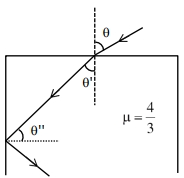
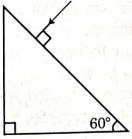
એક પ્રકાશનું કિરણ હવામાંથી $\frac{4}{3}$ વક્રીભવનાંક ધરાવતા મધ્યમમાં પ્રવેશે છે, તે આકૃતિમાં દર્શાવેલ છે. દર્શાવ્યા પ્રમાણે પ્રકાશનું કિરણ બાજુની સપાટી પાસે પૂર્ણ આંતરિક પરાવર્તન પામે છે. $\theta$ નું મહત્તમ મૂલ્ય કોને બરાબર થવું જોઈએ?

JEE MAIN 2021, Diffcult
b
At maximum angle \(\theta\) ray at point \(B\) goes in gazing emergence, at all less values of \(\theta, \operatorname{TIR}\) occurs.
At maximum angle \(\theta\) ray at point \(B\) goes in gazing emergence, at all less values of \(\theta, \operatorname{TIR}\) occurs.
At point B
\(\frac{4}{3} \times \sin \theta^{\prime \prime}=1 \times \sin 90^{\circ}\)
\(\theta^{\prime \prime}=\sin ^{-1}\left(\frac{3}{4}\right)\)
\(\theta^{\prime}=\left(\frac{\pi}{2}-\theta^{\prime \prime}\right)\)
At point \(A\)
\(1 \times \sin \theta=\frac{4}{3} \times \sin \theta^{\prime}\)
\(\sin \theta=\frac{4}{3} \times \sin \left(\frac{\pi}{2}-\theta^{\prime \prime}\right)\)
\(\sin \theta=\frac{4}{3} \cos \left[\cos ^{-1} \frac{\sqrt{7}}{4}\right]\)
\(\sin \theta=\frac{4}{3} \times \frac{\sqrt{7}}{4}\)
\(\theta=\sin ^{-1}\left(\frac{\sqrt{7}}{3}\right)\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$15\; cm$ કેન્દ્રલંબાઇના એક અંતર્ગોળ અરીસાથી $40\;cm$ પર એક વસ્તુ મુકેલ છે. જો આ વસ્તુને $20\;cm$ આ અરીસા તરફ ખસેડવામાં આવે, તો પ્રતિબિંબનું સ્થાનાંતર કેટલું હશે?View Solution
- 2$10\, cm$ કેન્દ્રલંબાઈના બહિર્ગોળ લેન્સથી $15\, cm$ દૂર પદાર્થ મૂકેલો છે. લેન્સની બીજી બાજુ લેન્સની કેન્દ્રલંબાઈ જેટલા અંતરે બહિર્ગોળ અરીસો એવી રીતે મૂકેલો છે. જેથી પ્રતિબિંબ પદાર્થને છેદે છે. તો બહિર્ગોળ અરીસાના કેન્દ્રલંબાઈ.......$cm$ થશે?View Solution
- 3અહીં દર્શાવેલ આકૃતિમાં લેન્સના સંયોજનની સમતુલ્ય કેન્દ્રલંબાઈ ($cm$ માં) કેટલી છે? (બધા જ સ્તરો પાતળા ધારો)View Solution
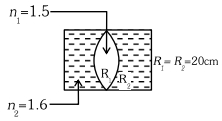
- 4સમાન બે પાતળા સમતલ બહિર્ગોળ લેન્સો (દ્રવ્યનો વક્રીભવનાંક $1.5$), દરેકની વક્રતાત્રિજયા $20\; cm $ છે, તેમને એક પાત્રમાં એવી રીતે મૂકેલા છે, કે જેથી તેમની બહિર્ગોળ સપાટી મધ્યમાં એકબીજાને સ્પર્શે. બાકીના ભાગમાં $1.7$ વક્રીભવનાંકવાળું ઓઇલ ભરવામાં આવે છે. આ સંયોજનની કેન્દ્રલંબાઈ ($cm$ માં) કેટલી થાય?View Solution
- 5ઉદગમ $L$ માંથી કિરણ $x$ અંતરે રહેલા સમતલ અરીસા પર લંબ પડે છે. કિરણ સ્ત્રોત ઉદગમ $L$ ની બરાબર ઉપર મૂકવામાં આવેલા સ્કેલ પર બિંદુ તરીકે પાછું પ્રતિબિંબિત થાય છે. હવે અરીસાને $\theta $ ખૂણે ફેરવતા આ બિંદુ સ્કેલ પર ઉપર તરફ $y $ જેટલા અંતરે ખસે છે. $\theta$ શેના વડે આપી શકાય?View Solution
- 6ઘટ્ટ માધ્યમનો પાતળા માધ્યમની સાપેક્ષે વક્રીભવનાંક $n_{12}$ અને તેનો ક્રાંતિકકોણ $\theta_C$ છે. જ્યારે પ્રકાશ ઘટ્ટ માધ્યમમાંથી પાતળા માધ્યમમાં ગતિ કરતો હોય ત્યારે તે સપાટી પાસે $A$ ખૂણે આપત થાય છે, જેમાંથી થોડોક ભાગ પરાવર્તન પામે છે અને બીજો ભાગ વક્રીભવન પામે છે. પરાવર્તિતકિરણ અને વક્રીભૂતકિરણ વચ્ચેનો ખૂણો $90^o$ હોય તો આપતકોણ $A$ કેટલો હશે?View Solution
- 7પાતળા પ્રિઝમનો વક્રીભવનાંક $1.5$ હોય,તો લઘુત્તમ વિચલન કોણ ${\delta _m}$ અને વક્રીભૂતકોણ $r$ વચ્ચેનો સંબંધ નીચે પૈકી કયો થાય?View Solution
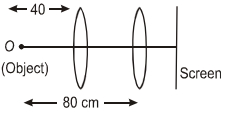
- 8સ્થાનાંતર રીતમાં સ્પષ્ટ પ્રતિબિંબ માટે લેન્સ બે સ્થાન છે. લેન્સનું પ્રથમ સ્થાન વસ્તુથી $40 \,cm$ અંતરે અને બીજુ $80 \,cm$ અંતરે છે, તો લેન્સની કેન્દ્રલંબાઈ ......... $cm$ છે.View Solution
- 9પ્રિઝમમાંથી નિકળતા નિર્ગમનકોણનું મૂલ્ય શોધો. ગ્લાસનો વક્રીભવનાંક $\sqrt{3}$ છે. ($^{\circ}$ માં)View Solution
- 10$10\,cm$ ની કેન્દ્રલંબાઈ ધરાવતા એક દ્વિ બહીર્ગોળ લેન્સને બે એકસમાન ભાગમાં એવી રીતે અલગ કરવામાં આવે છે કે જેની મુખ્ય અક્ષ તેના સમતલને લંબ રહે. અલગ કરેલા લેન્સોની શક્તિ .......... $D$ છે.View Solution
