From lens Maker's formula
\(\frac{1}{f}=(\mu-1)\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)\)
If \(f_{1}, f_{2}\) are focal lengths of two plano convex lenses, then
\(\therefore \frac{1}{f_{1}}=(1.5-1)\left(\frac{1}{20}-\frac{1}{\infty}\right)\)
\(\frac{1}{{{f_1}}} = (0.5)\left( {\frac{1}{{20}}} \right) = \frac{1}{{40}}\) \(\left[ {{\text{As}}\,\,{R_2}{\text{ is }}\infty } \right]\)
and \(\frac{1}{f_{2}}=(1.5-1)\left(\frac{1}{20}-\frac{1}{\infty}\right)=\frac{1}{40}\)
For concave lens of oil,
\(\frac{1}{{{f_3}}} = (1.7 - 1)\left( {\frac{{ - 1}}{{20}} + \frac{{ - 1}}{{20}}} \right)\) \( = 0.7 \times \frac{{ - 2}}{{20}} = \frac{{ - 7}}{{100}}\)
focal length of the combination is given by,
\(\frac{1}{f}=\frac{1}{f_{1}}+\frac{1}{f_{2}}+\frac{1}{f_{3}}\)
\(\frac{1}{f}=\frac{1}{40}+\frac{1}{40}+\left(\frac{-7}{100}\right)\)
\(=\frac{5+5-14}{200}=\frac{-4}{200}=\frac{-1}{50}\)
\(f=-50\, \mathrm{cm}\)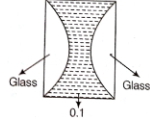
Download our appand get started for free
Similar Questions
- 1પ્રિઝમમાં $45^o $ ના આપાતકોણે કિરણ આપાત કરતાં લઘુત્તમ વિચલન મળે છે.પ્રિઝમનો વક્રીભવનાંક $\sqrt 2 $ હોય,તો પ્રિઝમનો પ્રિઝમકોણ કેટલા ....$^o$ હશે?View Solution
- 2$20 \,cm$ કેન્દ્રલંબાઈના અંતર્ગોળ અરીસાથી $40 \,cm$ દૂર પદાર્થ મૂકેલો છે તો રચાતું પ્રતિબિંબ ......છે.View Solution
- 3શરૂઆતમાં સમાંતર એવું નળાકાર કિરણજૂથ $\mu( I )=\mu_{0}+\mu_{2} I$ ધન વક્રીભવનાંકવાળા માધ્યમમાં પસાર થાય છે. અહી $\mu_{0}$ અને $\mu_{2}$ એ ધન અચળાંકો છે અને $I$ એ કિરણજૂથની તીવ્રતા છે. ત્રિજ્યામાં વધારા સાથે કિરણજૂથની તીવ્રતામાં ઘટાડો થાય છે.View Solution
આ માધ્યમમાં પ્રકાશની ગતિ
- 4$f$ કેન્દ્રલંબાઇ ધરાવતા અંર્તગોળ અરીસાને પાણી ($\mu = 4/3$) માં ડુબાડતાં નવી કેન્દ્રલંબાઇ કેટલી થાય?View Solution
- 5બે પારદર્શક માધ્યમો $A$ અને $B$ ને સમતલ સપાટી થી છૂટા પાડવામાં આવેલ છે. આ માધ્યમોમાં, પ્રકાશની ઝડપ અનુક્રમે $1.5 \times 10^{8} m / s$ અને $2.0 \times 10^{8} m / s$ છે. આ માધ્યમો માટે ક્રાતિ કોણ $......$ હશે.View Solution
- 6$A$ પ્રિઝમકોણ ધરાવતા પ્રિઝમની એક બાજુ પર ચાંદી લગાવેલ છે. એક બાજુ પર $2A$ ખૂણે કિરણ આપાત કરતાં ચાંદી લગાવેલ બાજુ પર પરાવર્તન પામીને મૂળ માર્ગે પાછું આવે છે. પ્રિઝમના પદાર્થનો વક્રીભવનાંક $\mu$ કેટલો હશે?View Solution
- 7$40 \,cm$ કેન્દ્રલંબાઈ ધરાવતા બે સરખા સમતલ-બહિર્ગોળ લેન્સની સમતલ બાજુને એકબીજાની સામે મૂકવામાં આવી છે, જેનાથી સામાન્ય બહિર્ગોળ લેન્સ રચાય છે. $-1$ મોટવણીનું ઊલટુ, વાસ્તવિક પ્રતિબિંબ મેળવવા વસ્તુને લેન્સથી ...... $cm$ અંતરે મૂક્વી જોઇેએ ?View Solution
- 8દિવાલથી $3 \,m$ અંતરે $3\, cm$ ઊંચાઇની મીણબત્તી મૂકેલી છે,દિવાલથી કેટલા......$cm$ અંતરે અંર્તગોળ અરીસો મૂકવાથી દિવાલ પર $9 \,cm$ ઊંચાઇનું પ્રતિબિંબ મળે?View Solution
- 9$1.5$ વક્રીભવનાંકના કાટના બનેલા $6^{\circ}$ પ્રિઝમકોણના પાતળા પ્રિઝમને $1.75$ વક્રીભવનાંકના કાંચના બનેલા બીજા પ્રિઝમ સાથે જોડીને વિચલન વગર વિભાજન કરવામાં આવે છે. તો બીજા પ્રિઝમનો પ્રિઝમકોણ કેટલો છે ?View Solution
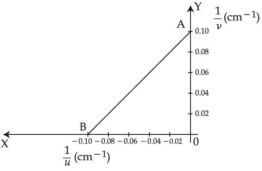
- 10એક પાતળા બહિર્ગોળ લેન્સની કેન્દ્રલંબાઈ શોધવા માટે $\frac{1}{ u}$ અને $\frac{1}{v}$ વચ્ચેનો આલેખ દર્શાવ્યા મુળબ દોરવામાં આવે છે. લેન્સનો વક્રીભવનાંક $1.5$ છે અને તેની બંને સપાટીને સમાન વક્રતા ત્રિજ્યા $(R)$ છે. $R$ નું મૂલ્ય $.........cm$ હશે.(જ્યાં $u =$ વસ્તુ અંતર, $v =$ પ્રતિબિંબ અંતર)View Solution