એક સ્થિર સ્થિતિમાં રહેલું પૈડું અચળ કોણીય પ્રવેગ થી ફરવાનું સારું કરે છે જો તે પ્રથમ $1\ sec$ માં $\theta_1 $ અને બીજી સેકંડ માં $\theta_2 $ કોણીય અંતર કાપે તો $\theta_2 \over \theta_1 $ =
Medium
c
Angular displacement in first one second \({\theta _1} = \frac{1}{2}\alpha \,{(1)^2} = \frac{\alpha }{2}\) ......\((i)\) [From \(\theta = {\omega _1}t + \frac{1}{2}\alpha \,{t^2}\)]
Angular displacement in first one second \({\theta _1} = \frac{1}{2}\alpha \,{(1)^2} = \frac{\alpha }{2}\) ......\((i)\) [From \(\theta = {\omega _1}t + \frac{1}{2}\alpha \,{t^2}\)]
Now again we will consider motion from the rest and angular displacement in total two seconds
\({\theta _1} + {\theta _2} = \frac{1}{2}\alpha \,{(2)^2} = 2\alpha \) ......\((ii)\)
Solving \((i)\) and \((ii)\), we get \({\theta _1} = \frac{\alpha }{2}\) and \({\theta _2} = \frac{{3\alpha }}{2}\) \(\therefore \) \(\frac{{{\theta _2}}}{{{\theta _1}}} = 3\).
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1આકૃતિમાં એક બેડમિન્ટન રેકેટના પરિમાણ આપેલા છે. જો બેડમિન્ટનના રેખીય અને વર્તુળાકાર ભાગનું સમાન દળ $(M)$ અને દોરીનું દળ અવગણ્ય હોય તો, હેન્ડલના બિંદુ $A$ થી $\frac{r}{2}$ અંતરે રેકેટના હેન્ડલને લંબ અને રિંગના સમતલમાં રહેલી અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા ....... $Mr^2$ જેટલી થાય?View Solution
- 2નિયમિત સળિયાનું દળ $ M$ અને લંબાઈ $ ℓ$ સળિયાને લંબ કેન્દ્રમાંથી પસાર થતી અક્ષ પર જડત્વની ચાકમાત્રા $ I$ છે. સળિયાના છેડામાંથી પસાર થતી અને સળિયાને લંબ અક્ષ પર જડત્વની ચાકમાત્રા કેટલી થશે ?View Solution
- 3View Solutionઘન ગોળાને મુક્ત અવકાશમાં ચાકગતિ કરે છે. જો ગોળાની ત્રિજ્યા વધારવામાં આવે અને તેનું દળ તેટલું જ રાખવામાં આવે તો નીચેનામાંથી .... ને અસર થશે નહિ.
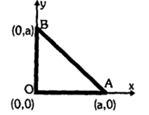
- 4View Solutionત્રણ સમાન દળના સળિયા આકૃતિમાં દર્શાવેલ છે. તંત્રના દ્રવ્યમાન કેન્દ્રના યામાક્ષ બિંદુઓ શોધો.
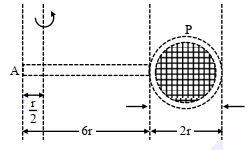
- 5$72\, km/h$ ની ઝડપથી જતી કારને બ્રેક મારતાં ટાયર $20$ પરિભ્રમણ પછી સ્થિર થાય છે.જો ટાયરનો વ્યાસ $0.5\, m$ હોય,તો કોણીય પ્રતિપ્રવેગ ($rad/s^2$ માં) કેટલો થાય?View Solution
- 6એક મિટર સ્કેલ નું સમતોલન $40 \,cm$ પર છે જ્યારે $10\, g$ અને $20 \,g$ ના પદાર્થને $10 \,cm$ અને $20\, cm$ પર મૂકેલા છે તો મિટર સ્કેલનું વજન ...... $g$ હશે ?View Solution
- 7$0.20\ kg - m^2$ અને $20\ cm$ ત્રિજ્યાના વ્હીલની રીમ પર દોરી વીટાળેલી છે. વ્હીલ તેની અક્ષ પર મુક્ત પણે ભ્રમણ કરે છે. અને વ્હીલ પ્રારંભમાં સ્થિર છે. દોરીને હવે $20\ N$ બળથી ખેચવામાં આવે છે. $5\ s$ બાદ દોરીનો કોણીય વેગ ......... $rad/s$ થશે.View Solution
- 8$(1)$ રિંગView Solution
$(2)$ તકતી
$(3)$ ઘન નળાકાર
$(4)$ ઘન ગોળો
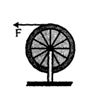
બધા જ પદાર્થોના દળ $m$ અને ત્રિજ્યા $R$ છે તેમને સમાન ઢાળ પરથી મુક્તા તે ગબડીને નીચે તળિયે આવે છે. તો પ્રથમ તળિયે કયા નંબરનો પદાર્થ આવશે?
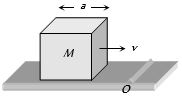
- 9$a$ બાજુવાળો એક સમઘન નીચેની આકૃતિમાં દર્શાવ્યા પ્રમાણે એક સમક્ષિતિજ સમતલ પર $v$ વેગથી ગતિ કરે છે તે $O$ બિંદુ આગળ આકૃતિમાં દર્શાવ્યા પ્રમાણે એક ઊપસેલી સપાટી પાસેથી પસાર થાય તો $O$ બિંદુ પછી તેનો કોણીય વેગ કેટલો થાય ?View Solution
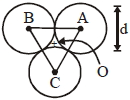
- 10$\mathrm{m}$ દળ અને $d$ વ્યાસ ધરાવતા ત્રણ ઘન ગોળા એવી રીતે જોડાયેલા છે કે જેથી તેમના કેન્દ્રને જોડતા તે $d$ લંબાઇનો સમબાજુ ત્રિકોણ બનાવે.જો $\mathrm{I}_{0}$ એ તેમના દ્રવ્યમાન કેન્દ્ર અને $\mathrm{I}_{\mathrm{A}}$ એ કોઇ એક ગોળાના કેન્દ્રમાથી અને ત્રિકોણના સમતલને લંબ અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા હોય તો $\mathrm{I}_{0} / \mathrm{I}_{\mathrm{A}}$ નો ગુણોત્તર કેટલો મળે?View Solution