એક ટેબલ તેના કેન્દ્રમાંથી પસાર થતી શિરોલંબ અક્ષની આસપાસ $20\ rad/s$ ના કોણીય વેગથી ભ્રમણ કરે છે તેની પોતાની ઉપર એક ફલાય વ્હીલ જોડેલું છે જેની સમક્ષિતિજ ધરી સાથે બેરિંગ જોડેલી છે તેની આસપાસ $40\ rad/s$ થી ભ્રમણ કરે છે. વ્હીલનો પરિણામી કોણીય વેગ..... હશે.
Medium
c
ટેબલની અક્ષ શિરોલંબ હોવાથી તેનો કોણીય વેગ શિરોલંબ દિશામાં હોય છે ફ્લાય વ્હીલની અક્ષ સમક્ષિતિજ દિશામાં છે માટે પરિણામી કોણીય વેગ,
ટેબલની અક્ષ શિરોલંબ હોવાથી તેનો કોણીય વેગ શિરોલંબ દિશામાં હોય છે ફ્લાય વ્હીલની અક્ષ સમક્ષિતિજ દિશામાં છે માટે પરિણામી કોણીય વેગ,
\( {\overline \omega _R}\,\, = \,\,{\overline \omega _F}\,\, + \,\,{\overline \omega _T} \)
\( |{\overline \omega _R}|\,\, = \,\,\sqrt {\omega _F^2 + \omega _T^2} \,\,\, = \,\,\sqrt {{{40}^2} + {{20}^2}} \,\, = \,\,20\sqrt 5 \,\,rad\,/\,\,s\)
\({\overline \omega _R}\,\) એ સમક્ષિતિજ સાથે \(\theta\) કોણ બનાવતા સમતલ માં રહે છે .
\(\theta\) વડે \(ta{n^{ - 1}}\,\,\left( {\frac{{{\omega _T}}}{{{\omega _F}}}} \right)\,\,\, = \,\,{\tan ^{ - 1}}\,\left( {\frac{1}{2}} \right)\)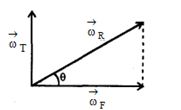
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$50\;m$ ત્રિજયા ધરાવતા પથ પર $ 500 \;kg$ ની કાર $36\;km/hr$ ની ઝડપથી વળાંક લે છે. કેન્દ્રગામી બળ .......... $N$ થાય.View Solution
- 2$1 \,kg$ દળનાં કોઈ પદાર્થ સમ ક્ષિતિજ સમાંતર સપાટી પર $8 \,m / s$ નાં પ્રારંભિકિ વેગ સાથે ગતિ કરીને $10\,s$ પછી અટકી જાય છે. જો કોઈ વસતુુને આ જ સપાટી પર $8 \,m / s$ નાં વેગ સાથે ગતિમાં રાખવાની ઈચ્છા રાખે છે તો તે માટે જરરી બળ ........... $N$ છેView Solution
- 3$'m '$ દળના એક પદાર્થ ને સ્પ્રિંગના એક છેડે બાંધીને સમક્ષિતિજ સમતલમાં અચળ કોણીય વેગથી ચક્રાકારે ફેરવવામાં આવે છે. સ્પ્રિંગમાં ખેંચાણ $1\, cm$ છે. જો કોણીય વેગ બમણો કરવામાં આવે તો સ્પ્રિંગમાં ખેંચાણ $5\, cm$ થાય છે. તો સ્પ્રિંગની મૂળ લંબાઈ ........ $cm$ હશે.View Solution
- 4View Solutionજ્યારે ઢાળ પર રહેલો પદાર્થ ગતિ ના કરે તો ઘર્ષણબળ ...
- 5View Solutionવિધાન: વિરામકોણ (Angle of repose) એ મર્યાદિત ઘર્ષણકોણ (limiting friction) ને બરાબર થાય.
કારણ: જ્યારે કોઈ પદાર્થ ગતિ કરવાની શરૂઆતની સ્થિતિ માં હોય ત્યારે ઘર્ષણ બળ એ મર્યાદિત ઘર્ષણ ની સ્થિતિમાં હોય.
- 6એક પદાર્થ સંપૂર્ણ લીસા સમાન $45^{\circ}$ પર રહેલા ઢાળવાળા સમતલ પરથી સરકવા માટેના સમયના $\mathrm{n}$ ગણો સમય ખરબચડા $45^{\circ}$ પર રહેલા ઢાળવાળા સમતલ પર લાગે છે. પ્રદાથ અને ઢાળવાળા સમતલની સપાટી વચ્ચેનો ગતિક ઘર્ષણાંક. . . . . . . .છે.View Solution
- 7$800 \mathrm{~kg}$ ની એક કાર $300 \mathrm{~m}$ ની ત્રિજ્યાં અને $30^{\circ}$ ના કોણવાળા ઢોળાવ વાળા રોડ ઉપર વળાંક લે છે. જો સ્થિતિ ઘર્ષણાંક $0.2$ હોય તો સુરક્ષિત રીતે ગાડી આ વળાંક લઈ શકે તે માટે મહત્તમ ઝડપ . . . . .હશે. $\left(\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^2, \sqrt{3}=1.73\right)$ લો.View Solution
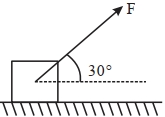
- 8આકૃતિમાં દર્શાવ્યા અનુસાર, સમક્ષિતિજ સપાટી ઉપર રહેલ $10\,kg$ ના દળને સમક્ષિતિજ સાથે $30^{\circ}$ ના કોણે $F$ બળથી ખેંચવામાં આવે છે.$\mu_{ s }=0.25$ માટે,બળ $F$ ના $........\,N$ મહતમ મૂલ્ય સુધી બ્લોક સ્થિર રહેશે.[$g=10\,ms^{-2}$ આપેલ છે.]View Solution
- 9દોરીના એક છેડે બાંધેલા $0.25\; kg$ દળના પથ્થરને સમક્ષિતિજ સમતલમાં $1.5 \;m$ $40\; rev./min$ ( પરિભ્રમણ/મિનિટ )ની ઝડપથી ઘુમાવવામાં આવે છે. દોરીમાં તણાવ કેટલું હશે ? જો દોરી મહત્તમ $200\; N$ નું તણાવ ખમી શકે તેમ હોય, તો કેટલી મહત્તમ ઝડપથી પથ્થરને ઘુમાવી શકાય ?View Solution
- 10ઢાળ પર પદાર્થ ને ઉપર ખસેડવા લગાવવું પડતું બળ તેને નીચે ખસેડતા અટકાવવા લગાવતા બળ કરતાં બમણું છે. જો ઘર્ષણાંક $0.25$ હોય તો ઢાળ નો ખૂણો ...... $^o$ હશે.View Solution
