એક ઉપગ્રહ પૃથ્વીની આજુબાજુ કક્ષીય વેગ ${v_0}$ થી ભ્રમણ કરે છે.જો તે એકાએક સ્થિર થઇ જાય અને પૃથ્વી પર અથડાઇ ત્યારે તેનો વેગ કેટલો થાય? (${v_e} = $ પૃથ્વીની સપાટી પરના નિષ્કમણ વેગ )
Diffcult
Download our app for free and get started
d
\( - \frac{{GMm}}{r} = \frac{1}{2}m{v^2} + \left( { - \frac{{GMm}}{R}} \right)\);
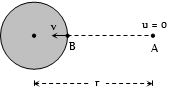
\( - \frac{{GMm}}{r} = \frac{1}{2}m{v^2} + \left( { - \frac{{GMm}}{R}} \right)\);
\(\frac{1}{2}m{v^2} = \frac{{GMm}}{R} - \frac{{GMm}}{r}\)
\({v^2} = \frac{{2Gm}}{R} - \frac{{2Gm}}{r}\)
\( = v_e^2 - 2v_0^2\)
\( \Rightarrow v = \sqrt {v_e^2 - 2v_0^2} \)[ \({v_e} = \sqrt {\frac{{2Gm}}{R}} \), \({v_0} = \sqrt {\frac{{Gm}}{r}} \)]
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1પૃથ્વીની સપાટી આગળના વજન કરતાં એક તૃત્યાંશ $\left(\frac{1}{3}\right)$ વજન થાય, તે પૃથ્વીની સપાટી થી ઉંચાઈ ....... $km$ હશેView Solution
[પૃથ્વી ની ત્રિજયા $R =6400\, km , \sqrt{3}=1.732$ ]
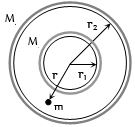
- 2સમકેન્દ્ર ગોળીય કવચના દળ ${M_1}$ અને ${M_2}$ છે. કેન્દ્રથી $r$ અંતરે આવેલા દળ $m$ પર ગુરુત્વતીવ્રતા કેટલી થાય?View Solution
- 3એક હલકો (નાનો) ગ્રહ એક મોટા (દળીય) તારાને ફરતે $R$ ત્રિજ્યામાં $T$ જેટલા પરિભમ્રણના આવર્તકાળ થી પરિભ્રમણ કરે છે. જો ગ્રહ અને તારા વચ્ચે પ્રવર્તંતું આકર્ષણબળ $R^{-3 / 2}$ સમપ્રમાણ છે તો સાચો વિકલ્પ પસંદ કરો.View Solution
- 4એક $90 \mathrm{~kg}$ ની વસ્તુને પૃથ્વીની સપાટીથી $2R$ અંતરે મૂકવામાં આવે છે કે જે. . . . . . . . . જેટલું ગુરુત્વાકર્ષી બળ અનુભવશે. $R$= પૃથ્વીની ત્રિજ્યા $\left.\mathrm{g}=10 \mathrm{~ms}^{-2}\right)$View Solution
- 5એક કણને ગ્રહથી ખૂબ દૂરના અંતરથી છોડવામાં આવે છે એે તે ગ્રહ આગળ માત્ર ગુરુત્વાકર્ષણના કારણે જ પહોંચે અને ગ્રહમાં એક ટનલ માંથી પસાર થાય છે. ગ્રહ પર પદાર્થનો નિષ્ક્રમણ વેગ $v _{ e }$ હોય તો, ગ્રહના કેન્દ્ર પર કણની ઝડપ કેટલી હશે?View Solution
- 6નીચે બે વિદ્યાનો આપેલા છે.View Solution
વિધાન $I$ : ગુત્વાકર્ષણનો નિયમ, કોઈપણ આકાર અને કદનાં, બ્રહ્માંડની કોઈ પણ વસ્તુની જોડ માટે સાચો છે.
વિધાન $II$ : વ્યક્તિ જ્યારે પૃથ્વીના કેન્દ્ર આગળ હોય ત્યારે તેનું વજન શૂન્ય થશે.
ઉપરોક્ત વિદ્યાનોનાં સંદર્ભમાં, આપેલા વિક્લોમાંથી સાચો ઉત્તર પસંદ કરો.
- 7$50\ kg $ નો માણસ ગુરુત્વમુકત અવકાશમાં જમીનથી $10\ m$ ઊંચાઇ પર છે. તે $0.5\ kg$ ના પથ્થરને $2\ m/s$ ની ઝડપથી નીચે તરફ ફેંકે છે. જ્યારે પથ્થર જમીન પર આવે, ત્યારે માણસનું જમીનથી અંતર ($m$ માં) કેટલું હશે?View Solution
- 8View Solutionજો ભ્રમણ કરતાં ઉપગ્રહની ત્રિજ્યા ઘટાડવામાં આવે, તો તેની ગતિ ઊર્જા .........
- 9પૃથ્વી પરના પદાર્થની નિષ્ક્રમણ ઝડપ આશરે .......... $km/sec$View Solution
- 10દરેક ગ્રહ સૂર્યની ફરતે લંબવૃત્તીય કક્ષામાં ગતિ કરે છે.View Solution
$A$. દરેક ગ્રહ પર લાગતું બળ સૂર્યથી અંતરના વર્ગના વ્યસ્ત પ્રમાણમાં હોય છે.
$B$. ગ્રહ પર લાગતું બળ ગ્રહ અને સૂર્યના દળના ગુણાકારના વ્યસ્ત પ્રમાણમાં હોય છે.
$C$. ગ્રહ પર લાગતું કેન્દ્રગામી બળ પૃથ્વીથી દૂરની દિશામાં હોય છે.
$D$. સૂર્યની ફરત ગ્રહના પરિભ્રમણ સમયનો વર્ગ લંબવૃત્તીય કક્ષાની અર્ધદીર્ધ અક્ષના ધનના સમપ્રમાણમાં હોય છે.
નીચે આપેલા વિકલ્પોમાંથી સાયો ઉત્તર પસંદ કરો.