\(R_1\) અવરોધમાંથી \(I_1\) અને \(R_2\) અવરોધમાંથી \(I_1\) પ્રવાહ પસાર થાય છે. તેમજ તેનો આંતરિક અવરોધ \(r\) છે.
\(\therefore \,\,\varepsilon \,\, = \,\,{I_1}\,({R_1} + r)\,\,\, \Rightarrow \,\,{I_1}\,\, = \,\,\frac{\varepsilon }{{{R_1} + r}}\)
\( \Rightarrow \,\,I_1^2{R_1}t\,\, = \,\,\frac{{{\varepsilon ^2}{R_1}t}}{{{{({R_1} + r)}^2}}}\,\, = \,\,{H_1}\)
\(\therefore \,\,\,\varepsilon \,\, = \,\,{I_2}\,({R_2} + r)\,\,\) \( \Rightarrow \,\,{I_2}\,\, = \,\,\frac{\varepsilon }{{{R_2} + r}}\,\)
\( \Rightarrow \,\,I_2^2{R_2}t\,\, = \,\,\frac{{{\varepsilon ^2}{R_2}t}}{{{{({R_2} + r)}^2}}}\,\, = \,\,{H_2}\)
પરંતુ \({{\text{H}}_{\text{1}}}\, = \,\,{H_2}\)
\(\therefore \,\,\frac{{{\varepsilon ^2}{R_1}t}}{{{{({R_1} + r)}^2}}}\,\, = \,\,\frac{{{\varepsilon ^2}{R_2}t}}{{{{({R_2} + r)}^2}}}\)
\( \Rightarrow \,\,\frac{{{R_1}}}{{{{({R_1} + r)}^2}}}\,\, = \,\,\frac{{{R_2}}}{{{{({R_2} + r)}^2}}}\)
\(\therefore \,\,{R_1}{({R_2} + r)^2}\,\, = \,\,{R_2}{({R_1} + r)^2}\,\)
\(\,\therefore \,\,\,\,\,\,{R_1}(R_2^2 + 2{R_2}.r\, + \,{r^2})\,\, = \,\,{R_2}(R_1^2 + 2{R_1}.\,r + {r^2})\)
\(\therefore \,\,{R_1}R_2^2\, + \,2{R_2}{R_2}r + {R_1}{r^2}\,\, = \,\,{R_2}R_1^2 + {R_1}{R_2}r + {R_2}{r^2}\,\,\,\)
\(\therefore \,\,\,\,\,({R_1} - {R_2}){r^2}\,\, = \,\,{R_2}{R_1}\,({R_1} - {R_2})\)
\(\therefore \,\,{r^2}\,\, = \,\,{R_1}{R_2}\,\, \Rightarrow \,\,r\,\, = \,\,\sqrt {{R_1} + {R_2}} \)
Download our appand get started for free
Similar Questions
- 1$\rho_L = 10^{-6}\, \Omega/m$ અવરોધકતાના તારને $2\ m$ વ્યાસના વત્રુળ સ્વરૂપમાં ફેરવવામાં આવે છે. સમાન પદાર્થના તારના ટુકડાને $AB$ વ્યાસમાં જોડવામાં આવે છે. તો $A$ અને $B$ વચ્ચે અવરોધ શોધો.View Solution
- 2જો તારને ખેંચીને $0.1 \%$ જેટલો લાંબો બનાવવામાં આવે તો તેનો અવરોધ.......હશે.View Solution
- 3View Solutionકોષનો આંતરિક અવરોધ એ કોનો અવરોધ છે?
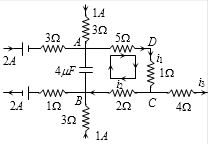
- 4View Solutionઆપેલ પરિપથના કેપેસિટરમાં કેટલી ઊર્જાનો સંગહ થાય?
- 5જો તાંબાના તારને તેની લંબાઈમાં $20\%$ વધારો મેળવવા માટે ખેંચવામાં આવે તો તેના અવરોધમાં $.............\%$ વધારો થાય.View Solution
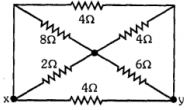
- 6$x$ અને $y$ ની વચ્ચેનો કુલ અવરોધ...... ઓહમ છે.View Solution
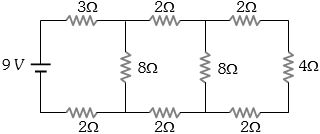
- 7View Solutionઆપેલ પરિપથમાં....
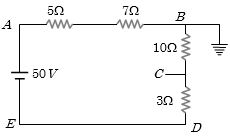
- 8કોષને $ 2\,Ω$ અવરોધ સાથે જોડતાં $0.5\, A $ અને $ 5\,Ω $ સાથે જોડતાં $0.25 \,A$ પ્રવાહ પસાર થાય છે,તો કોષનો $ emf$ કેટલા .............. $volt$ થાય?View Solution
- 9સમાન દ્રવ્ય ધરાવતા તારની ત્રિજયાનો ગુણોત્તર $1 : 2$ અને પ્રવાહનો ગુણોત્તર $4 : 1$ હોય,તો ડ્રિફટ વેગનો ગુણોત્તર કેટલો થાય?View Solution
- 10આપેલ પરિપથમાં $A$ બિંદુનો વોલ્ટેજ કેટલા .......... $V$ થાય?View Solution