\({P_0}{V_0} = nR{T_0}\)
\({P_0}V = NRT\)
\({T_f} = 2{T_0}\)
\(W = \int {PdV} \)
\( = \int {\left( {\frac{{nRT}}{V} + \alpha } \right)dV} \)
\(PV = nRT + \alpha V\)
\(\int {PdV = \int\limits_{{T_0}}^{2{T_0}} {nRdT + \int\limits_{{V_1}}^{{V_1}} {\alpha dV} } } \)
\( = nR{T_0} + \alpha \,{V_i}\)
\( = nR{T_0} + \alpha \left( {\frac{{nR{T_0}}}{{{P_0}}}} \right)\)
\( = nR{T_0} \left( {1 + \frac{\alpha }{{{P_0}}}} \right)\)
\(PV = nRT + \alpha V\)
\(\int {PdV = \int {nRdT + \int {\alpha dV} } } \)
\(W = nR{T_0} + \alpha \left[ {\frac{{nR{T_0}}}{{{P_0} - \alpha }}} \right]\)
\(W = nR{T_0}\left[ {1 + \frac{\alpha }{{{P_0} - \alpha }}} \right]\)
\( = n{R_0}{T_0}\left[ {\frac{{{P_0}}}{{{P_0} - \alpha }}} \right]\)
\( = \frac{{nR{T_0}{P_0}}}{{{P_0} - \alpha }}\)
Download our appand get started for free
Similar Questions
- 1બે સમાન દળ ધરાવતો વાયુ તાપીય સંતુલનમાં છે. જો તેના દબાણ ${P_a},\,{P_b}$ અને કદ ${V_a}$ અને ${V_b}$ છે તો તેમની વચ્ચેનો સાચો સંબંધ કયો થાય?View Solution
- 2ઠારણ વ્યવસ્થાનું તાપમાન ${T}_{2}=400\, {K}$ અને ઉષ્મા પ્રાપ્તિસ્થાનનું તાપમાન ${T}_{1}$ વચ્ચે એક ઉષ્મા એન્જિન કાર્ય કરે છે. તે ઉષ્મા પ્રાપ્તિ સ્થાનમાંથી $300 \,{J}$ ઉષ્મા લે છે અને ઠારણ વ્યવસ્થામાં $240\, {J}$ ઉષ્મા ગુમાવે છે. ઉષ્મા પ્રાપ્તિસ્થાનનું ન્યૂનતમ તાપમાન ($K$ માં) કેટલું હોવું જોઈએ?View Solution
- 3$ {27^o}C $ રહેલા તાપમાને એક આદર્શ વાયુનું સમોષ્મી સંકોચન કરી કદ મૂળ કદથી $ \frac{8}{{27}} $ ગણું થાય છે. જો $\gamma = \frac{5}{3}$ હોય, તો તાપમાનમાં ...... $K$ વધારો થાય?View Solution
- 4View Solutionવિધાન : સમતાપી વક્ર એકબીજા સાથે કોઈ એક બિંદુ પર છેદે
કારણ : સમતાપી પ્રક્રિયા ધીમી હોવાથી તેનો ઢાળ નાનો હોય
- 5$P$ દબાણ અને $V$ કદના એક પરમાણ્વિક વાયુને પ્રથમ સમતાપીય રીતે વિસ્તરણ કરીને કદ $2V$ સુઘી અને પછી સમોષ્મી રીતે કદ $16 V $ કરે છે. વાયુનું અંતિમ દબાણ કેટલું થશે? ($\gamma = \frac{5}{3}$ લો)View Solution
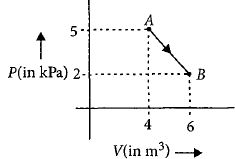
- 6એક મોલ દ્વિ પરમાણ્વિક આદર્શ વાયુ $A$ થી $B $ પર આકૃતિમાં બતાવ્યા મુજબ $AB $ માર્ગે જાય છે. આ ગતિમાં વાયુની આંતરિક ઊર્જાનો ફેરફાર ...............$kJ$ હશે.View Solution
- 7કોઈ ચોક્કસ થર્મોડાયનેમિક પ્રક્રિયામાં, વાયુનું દબાણ તેના પ્રારંભિક કદ પર $kV^3$ જેટલો આધાર રાખે છે. જ્યારે તાપમાન $100^{\circ} C$ થી $300^{\circ} C$ બદલવામાં આવે છે ત્યારે થતું કાર્ય ............$nR$ થશે, જ્યાં $n$ એ વાયુ માટે મોલ સંખ્યા દર્શાવે છે.View Solution
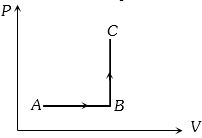
- 8$ A \to B \to C $ માટે તંત્ર દ્વારા થતું કાર્ય $30J$ અને તંત્ર દ્વારા શોષણ થતી ઉષ્મા $40J$ હોય,તો $A$ અને $C$ વચ્ચે આંતરિક ઊર્જામાં ...... $J$ ફેરફાર થશે?View Solution
- 9$27^{\circ}\,C$ તાપમાને અને $2 \times 10^7\,N / m ^2$ દબાણે રહેલા $V$ કદના અમુક જથ્થાનો વાયુ તેનું કદ બમણું ના થાય ત્યાં સુધી સમતાપીય વિસ્તરણ અનુભવે છે. પછી તે સમોષ્મી રીતે હજુ પણ કદ બમણું થાય તે રીતે વિસ્તરણ પામે છે. વાયુનું અંતિમ દબાણ $.......$ હશે. $(\gamma=1.5)$ લોView Solution
- 10જો ચક્રીય પ્રક્રિયામાં, $Q, E$ અને $W$ અનુક્રમે ઉમેરેલી ઉષ્મા, આંતરિક ઊર્જામાં ફેરફાર અને કરવામાં આવેલ કાર્ય દર્શાવે છે, તો ....View Solution
