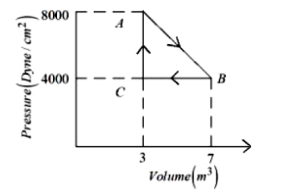
વિધાન : સમતાપી વક્ર એકબીજા સાથે કોઈ એક બિંદુ પર છેદે
કારણ : સમતાપી પ્રક્રિયા ધીમી હોવાથી તેનો ઢાળ નાનો હોય
JEE MAIN 2021, Medium
d
Isothermal curves have slope which is equal to \(\frac{P}{V}\). It can be calculated as follows \(PV = RT\) Differentiating, \(PdV + VdP = 0\) \(-\frac{dP}{dV} = \frac{P}{V}\) Now, if they cut each other at certain point, they will have different slope at the same point (for same value of \(P\) and \(V\)). So, they can not cut each other at some point. Reason is true, slope is \(\frac{P}{V}\) . For adiabatic curve slope is \(\gamma \) times \(\frac {P}{V}\) .
Isothermal curves have slope which is equal to \(\frac{P}{V}\). It can be calculated as follows \(PV = RT\) Differentiating, \(PdV + VdP = 0\) \(-\frac{dP}{dV} = \frac{P}{V}\) Now, if they cut each other at certain point, they will have different slope at the same point (for same value of \(P\) and \(V\)). So, they can not cut each other at some point. Reason is true, slope is \(\frac{P}{V}\) . For adiabatic curve slope is \(\gamma \) times \(\frac {P}{V}\) .
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1કાર્નોટ એન્જિન $727^°C$ અને $227^°C$ વચ્ચે કાર્ય કરે છે.કાર્નોટ એન્જિનની કાર્યક્ષમતા $\eta=$View Solution
- 2એક પરમાણ્વિક વાયુનું કદ $V$ , તાપમાન $T$ સાથે $V = KT ^{2 / 3}$ સંબંધ અનુસાર બદલાય છે. જ્યારે તાપમાન $90\, K$ જેટલું બદલાય ત્યારે થતું કાર્ય $x\,R$ છે. અહિંયા $x$ નું મૂલ્ય ......... છે. $[ R =$ વાયુ નિયતાંક].View Solution
- 3ઉષ્મીય એન્જિનને $300 \,cal$ ઉષ્મા આપવામાં આવે છે કે જેથી તે $225 \,cal$ ઉષ્મા ઠારણને આપે છે. જો ઉષ્માપ્રાપ્તિ સ્થાનનું તાપમાન $227^{\circ} C$ હોય તો ઠારણ વ્યવસ્થાનું તાપમાન ........... ${ }^{\circ} C$ હશે.View Solution
- 4પ્રતિવર્તી ઉષ્મા એન્જીન , એક ચર્તુથાંશ ઈનપુટ (આપાત) ઊર્જાનું કાર્યમાં રૂપાંતરણ કરે છે, જ્યારે ઠારણનું તાપમાન $52 \,K$ જેટલું ઘટાડવામાં આવે ત્યારે તેની કાર્યક્ષમતાં બે ગણી થાય છે. ઉદ્દગમનું કેલ્વીનમાં તાપમાન ......... હશે.View Solution
- 5એક દ્વિપરમાણ્વિક વાયુ $P V^{1.3}=$ અચળ વડે રજૂ કરેલ પ્રક્રિયામાંથી પસાર થાય છે. સાચુ નિવેદન પસંદ કરો.View Solution
- 6બે જુદા પથ ($ACB$ અને $ADB$) પરથી એક વાયુને $A$ થી $B$ સુધી લઈ જઈ શકાય છે. જ્યારે પથ $ACB$ અનુસરવામાં આવે ત્યારે પ્રણાલીમાં પ્રવેશતી ઉષ્મા $60\,J$ છે અને પ્રણાલી દ્વારા થતું કાર્ય $30\,J$ છે. જ્યારે પથ $ADB$ અનુસરવામાં આવે છે ત્યારે પ્રણાલી દ્વારા થતું કાર્ય $10\,J$ હોય તો આ પથ અનુસાર પ્રણાલીમાં પ્રવેશતી ઊષ્મા ........ $J$ હશે.View Solution
- 7પિસ્ટન ધરાવતા નળાકારમાં $27°C$ તાપમાને $0.2 \,mol$ હવા ભરેલી છે.સમતાપી પ્રક્રિયાથી અંતિમ કદ પ્રારંભિક કદથી બમણું કરતાં તંત્ર વડે ...... $J$ કાર્ય થાય.View Solution
- 8કોઈ તંત્ર $2 \,Kcal$ ઉષ્મા શોષીને $500\; J$ કાર્ય કરતું હોય, તો તંત્રની આંતરિક ઊર્જામાં ...... $J$ ફેરફાર થાય.View Solution
- 9એક રેફ્રિજરેટર $4^o C$ અને $30^o C$ તાપમાન વચ્ચે કાર્ય કરે છે. રેફ્રિજરેટરનું તાપમાન અચળ જાળવી રાખવા માટે તેમાંથી $600 $ કેલરી દર સેકન્ડે બહાર કાઢવી જરૂરી છે. આ માટે જરૂરી પાવર ......... $W$ ($1 $ કેલરી $=4.2$ જૂલ લો.)View Solution
- 10આકૃતિમાં દર્શાવ્યા મુજબ, એક થર્મૉડાયનેમિક તંત્રને રેખીય પ્રક્રિયા દ્વારા મૂલ સ્થિતિ $A$ માંથી મધ્યવર્તી સ્થિતિ $B$ માં લાવવામાં આવે છે. ત્યાર બાદ સમદાબ પ્રક્રિયા વડે તેનું કદ $B$ થી $C$ જેટલું ધટાડી મૂળ કદ જેટલું કરવામાં આવે છે. તો વાયુ દ્વારા $A$ થી $B$ અને $B$ થી $C$ સુધી લઇ જવા માટે કુલ કાર્ય_________થશે.View Solution