ગ્રહની સૂર્યની આસપાસ ઉત્કેન્દ્રતા $e$ વાળી દીર્ધવૃત્તીય કક્ષામાં ગતિ દરમિયાન ચંદ્રનીચ અને ચંદ્રોચ્ય બિંદુએ ગતિઊર્જાનો ગુણોતર શું છે ?
Medium
c
(c)
(c)
\(K.E\) of a planet \(=\frac{1}{2} m v^2\)
\(K.E\) at perigee \(=\frac{1}{2} m v_P^2\)
\(K.E\) at apogee \(=\frac{1}{2} m v_A^2\)
Using conservation of angular momentum at \(P\) and \(A\)
\(\Rightarrow m v_P r_P=m v_A r_A\)
\(\Rightarrow \frac{v_P}{v_A}=\frac{r_A}{r_P}=\frac{a(1+e)}{a(1-e)}\)
\(\Rightarrow \frac{ K \cdot E _P}{ K \cdot E _A}=\frac{v_P^2}{v_A^2}=\left(\frac{1+e}{1-e}\right)^2\)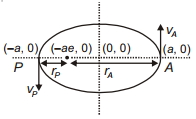
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionમાણસની પૃથ્વીની વિષુવવૃત્ત થી ધ્રુવ તરફની ગતિ દરમિયાન તેનું વજન એ ..... ( પૃથ્વીની ત્રિજ્યામાં થતો ફેરફાર અવગણો )
- 2બે ઉપગ્રહો $A$ અને $B$ અનુક્રમે $4R $ અને $R$ ત્રિજયામાં ભ્રમણ કરે છે. $A$ ઉપગ્રહનો વેગ $3V$ હોય,તો $B$ ઉપગ્રહનો વેગ ........ $V$ થાય.View Solution
- 3પૃથ્વી (પૃથ્વીનું દળ $M_E$ અને પૃથ્વીની ત્રિજયા $R_E$) ફરતે $3R_E$ ત્રિજયાના $m$ દળનો એક ઉપગ્રહ વર્તુળાકાર કક્ષામાં છે. આ ઉપગ્રહને $9R_E$ ત્રિજયાની કક્ષામાં લઈ જવા માટે વધારાની કેટલી ઊર્જાની જરૂરી પડે?View Solution
- 4એક ઉપગ્રહ $v$ જેટલી અચળ ઝડપથી એક વર્તુળાકાર કક્ષામાં પૃથ્વીની ફરતે ભ્રમણ કરે છે. એક $m$ દળ ધરાવતા પદાર્થને ઉપગ્રહ પરથી એવી રીતે ફેંકવામાં આવે છે કે જેથી તે પૃથ્વીના ગુરૂત્વાકર્ષણના ખેંચાણથી મુક્ત થાય. પદાર્થના મુક્ત કરવાના સમયે તેની ગતીઊર્જા કેટલી હશે?View Solution
- 5સૂર્યની આજુબાજુ ભ્રમણ કરતાં ગ્રહની કોણીય વેગમાન $J$ હોય,તો ગ્રહનો ક્ષેત્રીય વેગ કેટલો થાય?View Solution
- 6એક $90 \mathrm{~kg}$ ની વસ્તુને પૃથ્વીની સપાટીથી $2R$ અંતરે મૂકવામાં આવે છે કે જે. . . . . . . . . જેટલું ગુરુત્વાકર્ષી બળ અનુભવશે. $R$= પૃથ્વીની ત્રિજ્યા $\left.\mathrm{g}=10 \mathrm{~ms}^{-2}\right)$View Solution
- 7સૂર્યથી ઉલ્કાપિંડનું મહત્તમ અને લઘુતમ અંતર $1.6 \times 10^{12}\, m$ અને $8.0 \times 10^{10}\, m$ છે. સૂર્યથી નજીકના બિંદુએ ઉલ્કાપિંડનો વેગ $6 \times 10^{4}\, ms ^{-1}$ હોય તો સૂર્યથી દૂરના બિંદુએ ઉલ્કાપિંડનો વેગ .............. $\times 10^{3}\, m / s$ હશે.View Solution
- 8કોઇ ગ્રહ પર પદાર્થની નિષ્ક્રમણ ઝડપ $2\, km/s$ છે તો આ ગ્રહની સપાટીની નજીક પરિભ્રમણ કરતાં ઉપગ્રહનો કક્ષીય વેગ કેટલો થાય?View Solution
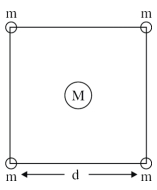
- 9$m$ દળ ધરાવતા ચાર ગોળાઓ $d$ બાજુ (આકૃતિમાં દર્શાવ્યા અનુસાર)નું ચોરસ બનાવે છે. એક પાંચમો $M$ દળ ધરાવતી ગોળો ચોરસના કેન્દ્ર આગળ મૂકવામાં આવે છે. તંત્રની કુલ સ્તિથિ ઊર્જા ........... થશે.View Solution
- 10બિંદુવત દળને પૃથ્વીની સપાટીથી $h$ ઊંંચાઈએ અને પૃથ્વીની સપાટીથી $\alpha h \left( h \ll < R _{ e }\right)$ જેટલી ઊંંડાઈએ ગુરુત્વાકર્ષણને કારણે ઉત્પન્ન પ્રવેગ સમાન અનુભવાય છે. $\alpha$ નું મૂલ્ય થશે.કારણે ઉત્પન્ન પ્રવેગ સમાન અનુભવાય છે. $\alpha$ નું મૂલ્ય થશે.$\text { ( } R _{ e }=6400\,km)$View Solution
