$h$ ઊંચાઇના ઢાળ પરથી ઘન નળાકાર મૂકતાં ચાકગતિઉર્જા અને કુલઉર્જાનો ગુણોત્તર
Medium
Download our app for free and get started
b
The cylinder has rotational \(KE = K _{1}=\frac{1}{2} Iw ^{2}\)
The cylinder has rotational \(KE = K _{1}=\frac{1}{2} Iw ^{2}\)
where \(I =\frac{ MR ^{2}}{2}\) about \(COM\) and \(w =\frac{ V }{ R }\)
\(\Rightarrow K _{1}=\frac{1}{2}\left(\frac{ M R ^{2}}{2}\right)\left(\frac{ V }{ R }\right)^{2}=\frac{1}{4} MV ^{2}\)
If it has a velocity of \(COM\), then translatory \(KE\) is \(K _{2}=\frac{1}{2} MV ^{2}\)
\(\therefore\) Total \(KE = K = K _{1}+ K _{2}=\frac{3}{4} MV ^{2}\)
Required ratio \(\frac{ K _{1}}{ K }=\frac{1 / 4 MV ^{2}}{3 / 4 MV ^{2}}=\frac{1}{3}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક પૈડાનો કોણીય પ્રવેગ $3\ rad/s^2$ છે. તેની પ્રારંભિક કોણીય ઝડપ $2\ rad/s $ છે, તો $2\ s$ માં તેણે કેટલું કોણીય સ્થાનાંતર ($rad$ માં) કર્યું હશે ?View Solution
- 2એક લીસો ગોળો $A$ ઘર્ષણરહીત સમક્ષીતિજ સપાટી પર કોણીય વેગ $\omega$ તથા દ્રવ્યમાન કેન્દ્રના વેગ સાથે ગતિ કરે છે. તે બીજા સમાન ગોળા $B$ સાથે સ્થીતિસ્થાપક સંઘાત અનુભવે છે. દરેક જગ્યાએ ઘર્ષણ અવગણતા સંઘાત બાદ તેમની કોણીય ઝડપ $\omega_A$ અને $\omega_B$ હોય તો......View Solution
- 3View Solutionઆકૃતિમાં કઇ અક્ષ પર કોણીય પ્રવેગ વધુ થશે અને બળ ત્રિકોણ ફ્રેમના મધ્યબિંદુ પર લાગે છે.
- 4$t = 0$ સમયે જમીન પરના બિંદુ $ P$ માંથી $m$ દળનો કણ $ v_0$ વેગથી $45^°$ ના ખૂણે સમિક્ષિતિજમાં પ્રક્ષેપિત કરવામાં આવે છે. $t\,\, = \,\,\frac{{{v_0}}}{g}$ સમયે કણનું કોણીય વેગમાનનું મૂલ્ય શોધો.View Solution
- 5કોઈ વ્હીલનો કોણીય પ્રવેગ $3.0\, rad/s^2$ અને પ્રારંભિક કોણીય ઝડપ $2.00\, rad/s$ છે. તો $2\, s$ સમયમાં તેણે કેટલું કોણાવર્તન(રેડિયનમા) કર્યું હશે?View Solution
- 6View Solutionએક વર્તુળાકાર તકતી લોખંડ અને એલ્યુમિનિયમમાંથી એવી રીતે બનાવવામાં આવે છે કે જેથી તેની તેની ભૌમિતિક અક્ષને લઈને તેની જડત્વની ચાકમાત્રા મહત્તમ થાય. આ કોની સાથે શક્ય છે?
- 7એક પૈડાને $1000\ N-m$ નું ટોર્ક આપતા તે તેના કેન્દ્રમાંથી પસાર થતા અક્ષની આસપાસ $200\ kg-m^2$ જડત્વની ચાકમાત્રા સાથે ફરે છે. તો $3 $ સેકન્ડ પછી પૈડાનો કોણીય વેગ $=$ ......... $\ rad/s$View Solution
- 8$1 \,kg$ દળ અને $R$ ત્રિજ્યા ધરાવતું એક ગોળાકાર કવચ (Shell) સમક્ષિતિજ સમતલ ઉપર (આકૃતિમાં દર્શાવ્યા અનુસાર) $\omega$ જેટલી કોણીય ઝડપ સાથે ગબડે છે. ઊગમબિંદુ $O$ ને સાપેક્ષ ગોળીય કવચના કોણીય વેગમાનનું મૂલ્ય $\frac{a}{3} R^{2} \omega$ છે. $a$ નું મૂલ્ય ............. હશે.View Solution
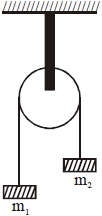
- 9આકૃતિમાં દર્શાવ્યા પ્રમાણે એક પાતળા ચક્રની ત્રિજ્યા $R$ અને જડત્વની ચાકમાત્રા $I$ છે જે પોતાના દ્રવ્યમાન કેન્દ્રને અનુલક્ષીને મુક્ત રીતે ફરી શકે છે.તેના પર બે દળ $\mathrm{m}_{1}$ અને $\mathrm{m}_{2}\left(\mathrm{m}_{1}>\mathrm{m}_{2}\right)$ ને દળરહિત દોરી દ્વારા લટકવેળા છે.જ્યારે તંત્રને સ્થિર સ્થિતિમાંથી મુક્ત કરવામાં આવે ત્યારે $\mathrm{m}_{1}$ દળ નીચે તરફ $h$ અંતર સુધી ગતિ કરે ત્યારે ચક્રની કોણીય ઝડપ કેટલી થશે?View Solution
- 10બે કણો સ્થિર પડેલા છે, આંતરિક બળોના કારણે તેઓ એકબીજા તરફ ગતિ કરે છે. જો કોઈ ક્ષણે તેમની ઝડપ $v$ અને $2v$ હોય, તો તંત્રના દ્રવ્યમાન કેન્દ્રનો વેગ કેટલો થાય?View Solution