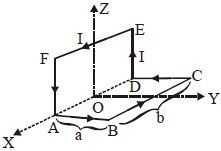
$I$ પ્રવાહધારિત તાર $A\,B\,C\,D\,E\,F\,A\,$ આપેલ છે. $A\,B\,C\,D\,A$ અને $A\,D\,E\,F\,A$ બાજુ એકબીજાને લંબ છે. લંબચોરસની બાજુની લંબાઈ $a$ અને પહોળાઈ $b$ છે. તો $A\,B\,C\,D\,E\,F\,A\,$ ની ચુબકીય મોમેન્ટ નું મૂલ્ય અને દિશા
JEE MAIN 2020, Diffcult
Download our app for free and get started
a
Sol. \(\quad M=N I A\)
Sol. \(\quad M=N I A\)
\(N =1\)
For \(ABCD\)
\(\overrightarrow{ M }_{1}= abI \hat{ K }\)
For \(DEFA\)
\(\overrightarrow{ M }_{2}= abI \hat{ j }\)
\(\overrightarrow{ M }=\overrightarrow{ M }_{1}+\overrightarrow{ M }_{2}\)
\(=\operatorname{ab} I (\hat{ k }+\hat{j})\)
\(=\operatorname{ab} I \sqrt{2}\left(\frac{\hat{j}}{\sqrt{2}}+\frac{\hat{ k }}{\sqrt{2}}\right)\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionટેસ્લા શેનો એકમ છે?
- 2એક ગેલ્વેનોમીટરને $200 \Omega$ નો અવરોધ અને તે $20 \mu \mathrm{A}$ પ્રવાહ માટે પૂર્ણ સ્કેલ આવર્તન આપે છે. તેને $(0-20) \mathrm{mA}$ ની રેન્જ (ગોળા)ના એમીટર તરીકે વાપરવું હોય તો તેમાં ઉમેરવો પડતો અવરોધ ......... થશે.View Solution
- 3ઇલેક્ટ્રોન $1.5 \times 10^{-2}\,T$ના ચુંબકીયક્ષેત્રમાં લંબ $6 \times 10^7\,m/s$નાં વેગથી દાખલ થાય છે.જો તેનો વિશિષ્ટ વિદ્યુતભાર $1.7 \times 10^{11}\,C/kg$ હોય,તો વર્તુળમય ગતિની ત્રિજ્યા ...... સેમીView Solution
- 4એક અર્ધવત્તુળાકાર રીંગના આકારનો આડછેદ ધરાવતાં અતિ લાંબા તારમાથી પ્રવાહ $I$ પસાર થાય છે. રીંગની ત્રિજ્યા $R$ છે. તો તારની અક્ષ પર ઉત્પન્ન થતા ચુંબકીય પ્રેરણનું મૂલ્ય કેટલું હશે?View Solution
- 5$50\, \Omega $ અવરોઘ ઘરાવતા ગેલ્વેનોમીટરને $2950\,\Omega$ અવરોઘ અને $3\,V $ ની બેટરી સાથે જોડેલ છે. ગેલ્વેનોમીટરમાં $30$ કાંપાનું પૂર્ણ સ્કેલ કોણાવર્તન મેળવવામાં આવે છે. આ કોણાવર્તનને $20$ કાંપા સુધી ઘટાડવા માટે તેની સાથે શ્રેણીમાં કેટલો અવરોઘ ($\Omega$) જોડવો પડે?View Solution
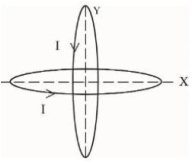
- 6બે $20\,cm$ ની સમાન ત્રિજ્યાવાળા તારો $\sqrt{2}\,A$ જેટલો વીજપ્રવાહ ધરાવે છે તેને સમતલમાં લંબરૂપે આકૃતિમાં દર્શાવ્યા પ્રમાણે મુકવામાં આવે છે. વર્તુળાકાર તારોના કેન્દ્રમાં પરિણામી ચુંબકીય ક્ષેત્ર $.......\times 10^{-8}\,T$છે.View Solution
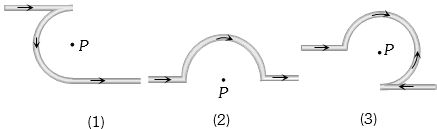
- 7નીચેની આકૃતિમાં $P$ બિંદુ આગળ ચુંબકીયક્ષેત્રનો ગુણોત્તર કેટલો થાય?View Solution
- 8એક લાંબા સોલેનોઇડને પ્રતિ સેમીમાં $70\,cm ^{-1}$ આટાં વીટાળીને બનાવવામાં આવે છે. જો તેમાંથી $2.0\,A$ પ્રવાહ વહે, તો સોલેનોઇડની અંદર ઉત્પન્ન થતું યુંબકીય ક્ષેત્ર $...............\times 10^{-4}\,T$ છે. $\left(\mu_o=4 \pi \times 10^{-7}\,T-mA ^{-1}\right)$View Solution
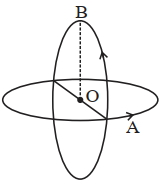
- 9આકૃત્તિમાં દર્શાવ્યા અનુસાર $'a'$ ત્રિજયા અને ઘડીયાળના કાંટાની વિરૂદ્ધ દિશામાં $'I'$ પ્રવાહ ધરાવતા બે અવાહક વર્તુળાકાર ગાળા $A$ અને $B$ ધ્યાનમાં લો. કેન્દ્ર આગળ ચુંબકીય પ્રેરણાનું મૂલ્ય___________થશે.View Solution
- 10View Solutionજો સ્પિંગમાંથી વિદ્યુતપ્રવાહ પસાર કરવામાં આવે, તો તે