જો દ્રવ્યનો વક્રીભવનાંક ‘$\mu $ ‘ છે. તેવા દ્રવ્યની સમતલ સપાટી પર હવામાંથી અધ્રુવીભૂત પ્રકાશ આપાત થાય છે.કોઇ ચોકકસ આપાતકાણે $‘i’$ પર એમ જોવા મળ્યું કે પરાવતિર્ત અને વક્રીભૂતકિરણો એકબીજાને લંબ છે.આ પરિસ્થિતિ માટે નીચેના વિધાનોમાંથી કયું સાચું છે?
NEET 2018, Medium
b
When reflected light and refracted light are perpendicular, reflected light is polarised with electric field vector perpendicular to the plane of incidence.
When reflected light and refracted light are perpendicular, reflected light is polarised with electric field vector perpendicular to the plane of incidence.
Also, \(tan\,\,i=\,\,\mu \) (Brewster angle)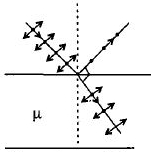
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionસાબુનો પાતળો પરપોટો રંગબેરંગી દેખાવાનું કારણ નીચેનામાથી કયું છે?
- 2યંગના બે સ્લિટના પ્રયોગમાં, $0.12\, mm$ અંતર ધરાવતી બે સ્લિટોથી $1\,m$ અંતરે શલાકાઓ બને છે. તો,પડદાને કેન્દ્રથી 3જી અપ્રકાશિત શલાકાનું અંતર.......$ cm$ શોધો. $\lambda$ $6000 \,Å$ આપેલ છે.View Solution
- 3$I_0$ તીવ્રતા ધરાવતા પ્રકાશ માટે પોલેરોઈડ $45^o$ ના કોણે ગોઠવેલો છે. તો હવે ધ્રુવીભવન પછી પોલેરોઈડમાંથી પસાર થતા પ્રકાશ માટે તીવ્રતા .....View Solution
- 4$6000\, Å$ ની તરંગલંબાઈ ધરાવતું સમતલ તરંગ અગ્ર $0.2 \,mm$ પહોળાઈ ધરાવતી સ્લીટ પર આપાત થાય છે કે જે ઉદ્દગમથી $2\, m$ અંતરે રહેલા પડદા પર ફ્રોનહોફર વિવર્તન ઉપજાવે છે તે કેન્દ્રીય મહત્તમની $mm$ માં પહોળાઈ કેટલી ?View Solution
- 5યંગના ડબલ સ્લીટના પ્રયોગમાં બે સ્લીટ વચ્ચેનું અંતર સ્લીટની જાડાઈ કરતાં $6.1$ ગણું છે. તો એક સ્લીટ દ્વારા થતાં વિવર્તનમાં મધ્યસ્થ અધિકતમની અંદર મહત્તમ તીવ્રતા કેટલી વખત દેખાશે?View Solution
- 6બે સુસમ્બધ્ધ પ્રકાશ ઉદગમો વ્યતિકરણ અનુભવે છે. બન્ને ઉદગમો તિવ્રતાનો ગુણોત્તર $1: 4$ છે. આ વ્યતિકરણ ભાત માટે $\frac{I_{\max }+I_{\min }}{I_{\max }-I_{\min }}$ એ $\frac{2 \alpha+1}{\beta+3}$ મળે છે,તો $\frac{\alpha}{\beta}$ $....$ થશે.View Solution
- 7યંગના દ્વિ સ્લીટ પ્રયોગમાં, આ સ્લીટો $2 \,mm$ ની છે અને તે બે તરંગલંબાઈ $\lambda= 7500 \,Å$ અને $\lambda = 9000\, Å$ ના મિશ્રણથી પ્રકાશિત કરેલ છે. સ્લીટથી $2 \,m$ દૂર પડદા ના સામાન્ય કેન્દ્રથી કેટલા......$mm$ અંતરે એક વ્યતિકરણ ભાતમાંની પ્રકાશિત શલાકા બીજામાંની પ્રકાશિત શલાકા સાથે સુસંગત થશે?View Solution
- 8યગ્રનાં ડબલ સ્લીટ પ્રયોગ માં એલ સ્લીટ બીજી કરતા વધારે પહોળી છે કે જેથી પહેલી સ્લીટમાંથી નીકળતા પ્રકાશને કંપ વિસ્તાર બીજીમાંથી નીકળતા પ્રકાશનાં કંપ વિસ્તાર કરતાં બમણો છે. જો $I_m$ મહત્તમ તિવ્રતા હોય તો જ્યારે તેઓ $\phi$ કળા તફાવતે વ્યતિકરણ પામે ત્યારે પરીણામી તિવ્રતા .............. વડે દર્શાવાય છે.View Solution
- 9બે તરંગો વચ્ચે કળા તફાવત $ \phi $ હોય,તો પથ તફાવત કેટલો થાય?View Solution
- 10બે સ્લિટ $1 \mathrm{~mm}$ ના અંતરે છે અને સ્લિટથી પડદો $1 \mathrm{~m}$ દૂર રહેલો છે. $500 \mathrm{~nm}$ તરગલંબાઈનો પ્રકાશ વાપરેલ છે. એક સ્તિરની ભાતના મધ્યસ્થ અધિક્તમમાં બે સ્લિટની ભાતના $10$ મહત્તમ સમાઈ જાય તે માટે પ્રત્યેક સ્લિટની પહોળાઈ. . . . . .$\times 10^{-4} \mathrm{~m}$ જોઈયે.View Solution
