\(\sqrt 2 \,\, = \,\,\frac{{\sin \,\,\left( {\frac{{60 + {\delta _m}}}{2}} \right)}}{{\sin \,\,\left( {\frac{{60}}{2}} \right)}}\)
\(\sqrt 2 \,\, \times \,\,\sin \,30\,\, = \,\,\,\sin \,\,\left( {\frac{{60 + {\delta _m}}}{2}} \right)\,\,\, \Rightarrow \,\,\,\,\sqrt 2 \,\, \times \,\,\,\frac{1}{2}\,\, = \,\,\sin \,\,\left( {\frac{{60 + {\delta _m}}}{2}} \right)\)
\(\sin \,\,{45^ \circ }\, = \,\,\sin \,\,\left( {\frac{{60 + {\delta _m}}}{2}} \right)\,\,\,\,\,\, \Rightarrow \,\,\,{45^ \circ }\,\, = \,\,\,\frac{{60 + {\delta _m}}}{2}\,\,\, \Rightarrow \,\,\,{\delta _m} = \,\,{30^ \circ }\)
\({\delta _m} = \,\,2i\,\, - \,\,A\,\,\, \Rightarrow \,\,30\,\, = \,\,2\,\,i\,\, - \,\,60\,\,\, \Rightarrow \,\,\,i\,\, = \,\,{45^ \circ }\)
Download our appand get started for free
Similar Questions
- 1View Solutionપાછળની બાજુએ જોવાના અરીસા માટે દિવસ અને રાતની ગોઠવણીઓ શેનો ઉપયોગ કરે છે ?
- 2View Solutionસમતલ અરીસાના કેન્દ્રલંબાઈ .......છે.
- 3એક માણસ $40\,\, cm$ થી વધુ અંતરે મૂકેલા પદાર્થને સ્પષ્ટ જોઈ શકાતો નથી. તેને કેવા પાવરના લેન્સની સલાહ આપેલી હશે?View Solution
- 4ગેલિલીયન ટેલિસ્કોપના વસ્તુકાંચ અને નેત્રકાંચની કેન્દ્રલંબાઈ અનુક્રમે $30\, cm$ અને $3.0\, cm$ છે. ટેલિસ્કોપથી દૂર પડેલી વસ્તુનું આભાસી અને મોટું પ્રતિબિંબ નેત્રકાંચથી નજીકતમ બિંદુ આગળ મળે છે. તો આ કિસ્સામાં ટેલિસ્કોપની મોટવણી કેટલી મળશે?View Solution
- 5સમતલ અરીસા પર કિરણ આપાત થાય છે,જો અરીસાને $\theta$ ના ખૂણે ફેરવતા પરાવર્તીત કિરણનું વિચલન કેટલું થાય?View Solution
- 6સંયુક્ત માઇક્રોસ્કોપના વસ્તુકાંચ અને નેત્રકાંચની કેન્દ્રલંબાઈ અનુક્રમે $1.2\, cm$ અને $3.0\, cm$ છે. જો વસ્તુને વસ્તુકાંચથી $1.25\, cm$ અંતરે મૂકવામાં આવે તો અંતિમ પ્રતિબિંબ અનંત અંતરે મળે છે. તો આ સંયુક્ત માઇક્રોસ્કોપની મોટવણી કેટલી હશે?View Solution
- 7View Solutionર્ફ્રોનહોફર સ્પ્રેક્ટલ એ
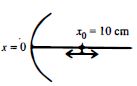
- 8$x_0 = 10\, cm$ પર રહેલ એક કણ $X-$ અક્ષ પર $2\, cm$ ના કંપવિસ્તાર અને $\omega $ આવૃતિથી દોલનો કરે છે.આકૃતિમાં દર્શાવ્યા પ્રમાણે એક $5\,cm$ કેન્દ્રલંબાઈ ધરાવતો અંતર્ગોળ અરીસો ઉગમબિંદુ પાસે છે. તો નીચે પૈકી કયા વિષનો સાચા પડશે.View Solution
$(A)$ પ્રતિબિંબ આવર્તનીય ગતિ કરે
$(B)$ પ્રતિબિંબ આવર્તનીય ગતિ કરશે નહીં
$(C)$ પ્રતિબિંબના મહત્તમ અને ન્યૂનતમ અંતર $x =10\,cm$ સાપેક્ષે અસંમિત હશે
$(D)$ પ્રતિબિંબના મહત્તમ અને ન્યૂનતમ અંતરનો તફાવત $\frac{{100}}{{21}}$ જેટલો હશે
- 9$100\,w$ ના લેમ્પની જ્યોતિ તીવ્રતા $100\,cd$ લેમ્પ દ્રારા કુલ જ્યોતિ ફ્લ્ક્ષ ......... $lumen$View Solution
- 10View Solutionજો ઓબ્જિેકિટવ લેન્સની કેન્દ્રલંબાઇ વધારવામાં આવે, તો ....
