જ્યારે $6.80 \,g$ $NH_3$ ને ગરમ $CuO $ પરથી પસાર કરવામાં આવે તો એન્થાલ્પીનો ફેરફાર કેટલો થાય $?$ અહિ $NH_3$ $_{(g)}$, $CuO$$_{(s)}$ અને $H_2O$$_{(l)}$ ની પ્રમાણિત એન્થાલ્પી ઉષ્મા અનુક્રમે $-46.0$, $55.0$ અને $-285.0\, kJ\, mol$ $^{-1}$ છે. અને પ્રક્રિયા,
$N{H_{3(g)}}\, + \,\,\frac{3}{2}\,Cu{O_{(s)}}\, \to \,\,\frac{1}{2}\,{N_{2(g)}}\, + \,\,\frac{3}{2}{H_2}{O_{(\ell )}}\, + \,\,\frac{3}{2}\,C{u_{(s)}}.$ ......$J$
Diffcult
Download our app for free and get started
c
$\,N{H_{3(g)}}\, + \,\,3/2Cu{O_{(s)}}\, \to \,\,1/2{N_{2(g)}}\,\, + \,\,3/2{H_2}{O_{(l)}}\, + \,\,3/2\,C{u_{(s)}}$
$\,N{H_{3(g)}}\, + \,\,3/2Cu{O_{(s)}}\, \to \,\,1/2{N_{2(g)}}\,\, + \,\,3/2{H_2}{O_{(l)}}\, + \,\,3/2\,C{u_{(s)}}$
$\Delta \,H\,\, = \,\,\Sigma \,\,{H_{\ Products}}\,\, - \,\,\,\Sigma \,{H_{\operatorname{Reactants}}}$
$\because \,\,H_{element}^ \circ \,\, = \,\,0$
$\therefore \,\,\Delta \,H\,\, = \,\,\frac{3}{2}\,H_{{H_2}O}^o \,\, - \,\,H_{N{H_3}}^o \, - \,\,\frac{3}{2}\,H_{CuO}^o $
$ = \,\,\frac{3}{2}\,\, \times \,\,( - 285)\, - \,( - 46)\, - \,\,\frac{3}{2}\,( - 155)\,\,\,\,\,\,\,\,\,\,\, = \,\, - 149\,\,KJ$
$\because \,\,17\,\,gm\,\,N{H_3}$ ના ફેરફાર જોતાં $\Delta \,\,H\,\, = \,\, - \,149\,\,KJ$
$\,6.8\,\,gm\,\,N{H_3}\,$ ના ફેરફાર જોતાં $\Delta H\,\, = \,\, - \frac{{149}}{{17}}\,\, \times \,\,6.8\,\,KJ$
$ = \,\, - 59.6\,\,KJ\,\,\,\,\,\,\,\,\,\,\,\Delta \,H\,\, = \,\, - \,\,59.6\,\,KJ$
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionદ્રાવણમાંં દ્રાવકને ઉમેરવાથી દ્રાવણની ઉષ્માનું મુલ્ય ...... છે.
- 2$0\,^oC$ થી $100\,^oC$ સુધી $128\, g$ ઓક્સિજન વાયુને ગરમ કરતાં તેનાં $C_v$ અને $C_p$ નાં સરેરાશ $5$ અને $7 \,cal\, mol ^{-1}$ અંશ$^{-1}$ છે. તો $\Delta U$ અને $\Delta H$ ના અનુક્રમે મૂલ્ય શોધો.View Solution
- 3અચળ તાપમાને અને દબાણે થતી નીચેની પ્રક્રિયા ધ્યાનમાં લો.View Solution
${N_2} + 3{H_2} \to 2N{H_3}$
જો $\Delta H$ અને $\Delta U$ અનુક્રમે પ્રક્રિયા માટેના એન્થાલ્પી ફેરફાર અને આંતરિક ઊર્જા ફેરફાર હોય, તો નીચેનામાંથી કઇ રજૂઆત સાચી છે ?
- 4કાર્બન મોનોક્સાઇડનુ કાર્બન ડાયોક્સાડમાં રૂપાંતર કરવા બે મોલ $C{O_{\left( g \right)}}$ અને એક મોલ ${O_2}_{\left( g \right)}$ નુ મિશ્રણ સળગાવવામાં આવે છે. તો નીચેનામાંથી ક્યો સંબંધ સાયો છે ?View Solution
- 5$H_2$$O$ $_{(l)}$ $(1 \,bar, 373 \,K)$ $\rightarrow$ $H_2O$ $_{(g)}$ $(1 \,bar, 373\, K)$, પ્રક્રિયા માટે ઉષ્માગતિશાસ્ત્રના પરિબળનો સાચો ક્રમ .......View Solution
- 6$25^o$ સે તાપમાને $\Delta H < T \Delta S $ તો $\Delta G$ = ………View Solution
- 7નીચેની માહિતી પરથી પ્રવાહી પાણીના બાષ્પીભવન એન્થાલ્પી .....$KJ \,mol^{-1}$ થશે :View Solution
$H_2$$_{(g)} +$ $1/2O_2$ $_{(g)}$ $\rightarrow$ $H_2$$O$$_{(l)}$; $\Delta H= -$ $285.77\, KJ\, mol$$^{-1}$; $H_2$$_{(g)} +$ $1/2O_2$$_{(g)}$ $\rightarrow$ $H_2O$ $_{(g)}$; $\Delta H$ $ = - 241.84\, KJ \,mol$$^{-1}$
- 8પ્રક્રિયા $A \to B$ માટે $\Delta H = 4\,kcal\,mo{l^{ - 1}}$ અને $\Delta S = 10\,cal\,{K^{ - 1}}\,mo{l^{ - 1}}$ હોય, તો પ્રક્યિા .......$K$ તાપમાને સ્વયંભૂ હોઇ શકે ?View Solution
- 9કઈ પ્રક્રિયા $\Delta H_f^o$ને વ્યાખ્યાયિત કરે છે.View Solution
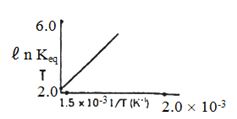
- 10પ્રક્રિયા માટે $ℓ\,n\, K_{eq}$ વિરૂદ્ધ તાપમાનનો આલેખ દોરવામાં આવે તો પ્રક્રિયા...... હોવી જોઈએ.View Solution
