માર્ગથી લઈ જવામાં આવે ત્યારે $Q = 50\, cal$ અને $W = 20\, cal$ મળે અને $ibf$ માર્ગ પર $Q = 36\, cal.$ છે
$(i)$ $ibf$ માર્ગ પર કાર્ય $W$ કેટલું હશે?
$(ii)$ જો $fi$ માર્ગ પર $W = 13\;cal$ હોય તો આ માર્ગ પર $Q$ કેટલો હશે?
$(iii)$ જો $E_{int,i} = 10\,\, cal$ હોય તો $E_{int,f}$ કેટલો હશે?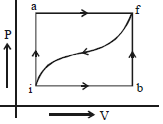
For path iaf
\(Q=50 \mathrm{cal}\)
\(\mathrm{W}=20 \mathrm{cal}\)
According ot I law of thermodynamics,
\(\mathrm{dQ}=\mathrm{dU}+\mathrm{d} \mathrm{W}\)
\(\text { or } \mathrm{dU}=\mathrm{dQ}-\mathrm{dW}=50-20=30 \mathrm{cal}\)
(1) For path iaf
\(Q=36\,cal\)
\({W=?}\)
\(\mathrm{dU}=30 \mathrm{cal}(\) since internal energy depends only on the initial and final positions of the system).
\(\therefore W=Q-d U=36-30=6 \mathrm{cal}\)
\(\begin{aligned} \text { (u) } \mathrm{W}=-13 \mathrm{cal} \\ \mathrm{d} \mathrm{U}=-30 \mathrm{cal} \\ \mathrm{Q}=? \end{aligned}\)
\(\therefore \mathrm{Q}=\mathrm{dU}+\mathrm{W}=-43 \mathrm{cal}\)
(iii) \(\quad \mathrm{E}_{\text {int }, \mathrm{f}}=\mathrm{E}_{\text {int }, i}+\Delta \mathrm{U}=10 \mathrm{cal}+30 \mathrm{cal} .=40\)
cal.
Download our appand get started for free
Similar Questions
- 1નીચેના આલેખમાં થર્મોડાયનેમિક પ્રક્રિયાઓ દર્શાવેલ છે.View Solution
આપેલ સ્તંભને મેળવો.
સ્તંભ - $1$ સ્તંભ - $2$ $P$< પ્રક્રિયા - $I$ $A$ : સ્મોષ્મિ $Q$ પ્રક્રિયા - $II$ $B$ : સમદાબ $R$ પ્રક્રિયા - $III$ $C$ : સમકદ $S$< પ્રક્રિયા - $IV$ $D$ : સમતાપી 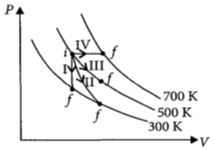
- 2આદર્શ વાયુ $A$ અવસ્થામાંથી $B$ અવસ્થામાં $ 8 \times {10^5}J $ ઉષ્માનું શોષણ કરીને કાર્ય $ 6.5 \times {10^5}J $ દ્વારા જાય છે. હવે,આદર્શ વાયુને બીજી પ્રક્રિયા દ્વારા અવઅથા $A$ માંથી અવસ્થા $B$ માં $ {10^5}J $ ઉષ્માનું શોષણ કરીને જતી હોય,તો કેટલું કાર્ય થાય?View Solution
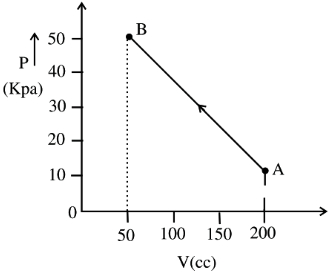
- 3આકૃત્તિમાં દર્શાવ્યા અનુસાર વાયુનું દબાણ કદ સાથે રેખીય રીતે $A$ થી $B$ સુધી બદલાય છે. જો કોઈપણ પ્રકારની ઉષ્મા આપવામાં આવતી ના હોય કે વાયુમાંથી શોષાતી ના હોય, તો વાયુની આંતરિક ઊર્જામાં થતો ફેરફાર $............\,J$ થશે.View Solution
- 4એક દૃઢ દ્રિપરમાણ્વીક આદર્શ વાયુ પૂરતા ઊંચા તાપમાને એક સમોષ્મી પ્રક્રિયામાંથી પસાર થાય છે. આ પ્રક્રિયા માટે તાપમાન અને કદનો સબંધ $TV^x =$ અચળ છે, તો $x$ કેટલો હશે?View Solution
- 5View Solutionસમતાપી પ્રક્રિયાનો આલેખ કયો છે.
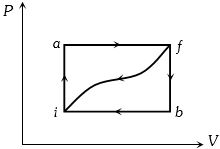
- 6તંત્ર અવસ્થા $i$ માંથી અવસ્થા $f$ માં $iaf$ માર્ગ માટે $ Q = 50\,J $ અને $ W = 20J. $ છે. માર્ગ $ibf$ માટે $ Q = 35J. $ છે. માર્ગ $fi$ માટે $ W = - 13J $ હોય,તો $Q =$........ $J$View Solution
- 7View Solutionનીચેનામાંથી શું પદાર્થની થરર્મોડાઇનેમિકસ અવસ્થાની લાક્ષણિકતા નથી?
- 8પાત્રમાં રહેલ આદર્શ વાયુને પિસ્ટન દ્વારા અલગ કરવામાં આવે છે,એક ભાગની એન્ટ્રોપી $S_{1}$ અને બીજા ભાગની એન્ટ્રોપી $S_{2}$ છે, $S _{1}> S _{2}$ જો પિસ્ટનને દૂર કરવામાં આવે તો તંત્રની કુલ એન્ટ્રોપી શું થશે?View Solution
- 9$1$ વાતાવરણ દબાણે $1 mm^{3} $ કદ ધરાવતા વાયુને તાપમાન $27°C$ થી $627°C$ સુધી દબાવવામાં આવે છે. સમોષ્મી પ્રક્રિયા પ્રમાણે અંતિમ દબાણ કેટલું હશે ? (વાયુ માટે $\gamma = 1.5$)View Solution
- 10એક કિલો મોલ વાયુનું સમોષ્મી સંકોચન કરવા માટે $146\; kJ$ કાર્ય કરવું પડે છે. આ પ્રક્રિયામાં વાયુંનું તાપમાન $7^{0} C$ વધતું હોય, તો આ વાયુ કેવો હોય? $\left(R =8.3 J mol ^{-1} K ^{-1}\right)$View Solution
