જ્યારે પ્રવાહ $A$ થી $B$ તરફ વહેતો હોય ત્યારે નીચે પૈકી ચાર અવરોધ $P, Q, R$ અને $S$ માથી કયો અવરોધ મહત્તમ ઉષ્મા ઉત્પન્ન કરે?
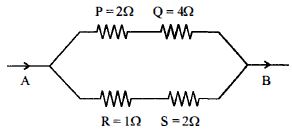

JEE MAIN 2013, Diffcult
b
\(\mathrm{R}_{1}=\mathrm{P}+\mathrm{Q}=2 \,\Omega+4\, \Omega=6 \,\Omega\)
\(\mathrm{R}_{1}=\mathrm{P}+\mathrm{Q}=2 \,\Omega+4\, \Omega=6 \,\Omega\)
\(\mathrm{R}_{2}=\mathrm{R}+\mathrm{S}=1 \,\Omega+2 \,\Omega=3\, \Omega\)
\(\mathrm{I}_{1} \mathrm{R}_{1}=\mathrm{I}_{2} \mathrm{R}_{2}\)
\(\mathrm{I}_{1}=\frac{\mathrm{R}_{2}}{\mathrm{R}_{1}} \mathrm{I}_{2}=\frac{3}{6} \mathrm{I}_{2}=\frac{\mathrm{I}_{2}}{2}\)
or \(\mathrm{I}_{2}=2 \mathrm{I}_{1}\)
Heat flow \(\mathrm{H}=\mathrm{I}^{2} \mathrm{Rt}\)
For \(Q, H_{Q}=I_{1}^{2} Q t=\frac{I_{2}^{2}}{4} \times 4 t=I_{2}^{2} t\)
For \(\mathrm{S}, \mathrm{H}_{\mathrm{S}}=\mathrm{I}_{2}^{2} \mathrm{St}=\mathrm{I}_{2}^{2} \cdot 2 \mathrm{t}=2 \mathrm{I}_{2}^{2} \mathrm{t}\)
\(\therefore \) Greatest amount of heat generated by \(S\).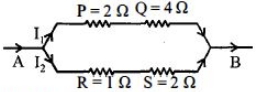
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionઆપેલ પરિપથમાં....
- 2$1.0\, m$ લંબાઇ અને $0.6\, cm $ વ્યાસ ધરાવતા તારનો અવરોધ $3.0 \times 10^{-3}\,Ω$ છે.સમાન દ્રવ્યમાંથી બનાવેલ $2.0\, cm $ વ્યાસ અને $1.0\, mm$ જાડાઇ ધરાવતી તકતી વચ્ચેનો અવરોધ કેટલો થાય?View Solution
- 3આપેલ પરિપથમાં આદર્શ વોલ્ટમીટર $(V)$ નું અવલોકન (રીડીંગ)_______છે.View Solution
- 4એક વાહકમાં એકમ કદ દીઠ $8.5 \times 10^{28}\, m^{-3}$ વાહક ઈલેક્ટ્રોન છે જેનો સરેરાશ રેલેક્સેશન સમય $25\,fs$ (ફેમટો સેકન્ડ),હોય તો તેની અવરોધકતા લગભગ કેટલી હશે? $\left( {{m_e} = 9.1 \times {{10}^{ - 31}}\,kg} \right)$View Solution
- 5$2\,Ω$ અવરોધ ધરાવતા ત્રણ અવરોધો $ P,Q $ અને $R$ ને વ્હીસ્ટન બ્રિજથી ત્રણ ભુજાઓમાં જોડેલા છે.બ્રિજની ચોથી ભુજામાં અવરોધ $S$ જોડેલ છે.જયારે $S$ ને સમાંતર $6\,Ω$ નો અવરોધ જોડવામાં આવે છે,ત્યારે બ્રિજ સંતુલિત થાય છે,તો અવરોધ $S$ નું મૂલ્ય ............... $\Omega$View Solution
- 6હિટર કોઈલ સાથે શ્રેણીમાં જોડેલ $50\,W$ બલ્બને $AC$ મુખ્યમાં મુકવામાં આવે છે. હવે જો બલ્બના $100\,W$ ના બલ્બ વડે બદલવામાં આવે તો, હિટરનું આઉટપુટ શું હોઈ શકે?View Solution
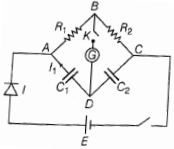
- 7આકૃતિમાં કળ $K$ બંધ કરતાં ગેલ્વેનોમીટરમાં પ્રવાહ પસાર થતો નથી. પરિપથ સંતુલન સ્થિતિમાં રહેલા માટેની શરત શું હશે?View Solution
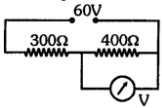
- 8નીચેના પરિપથમાં બતાવ્યા મુજબ $400\,\Omega$ અવરોધનો બે છેડા સાથે જોડેલ વોલ્ટ મીટરનું અવલોકન (વાંચન) $30\,\ V$ છે. તેને $300\, \Omega$ ના અવરોધ સાથે જોડવામાં આવે તો તેનું વાંચન ................ $V$ હશે.View Solution
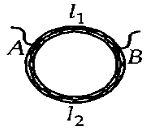
- 9$12\,\Omega $ અવરોધ ધરાવતા એક તારમાથી રીંગ બનાવવામાં આવે છે. આકૃતિમાં બતાવ્યા પ્રમાણે $A$ અને $B,$ બિંદુઓ શોધો, કે જેના પર પ્રવાહધારીત વાહક જોડાયેલ હોવો જોઈએ જેથી આ બિંદુઓ વચ્ચેના પરિપથનો અવરોધ $R=\frac {8}{ 3}\;\Omega$ જેટલો થાય?View Solution
- 10અહિંયા ઘણાં બધા કોષો હાજર છે. દરેકનો રેટીંગ $(6\,V$ $0.5$ $\Omega$) ઉપયોગ $0.75 \Omega$ અવરોધ,$24\,A$ વિદ્યુતપ્રવાહની જરૂરીયાત ધરાવતાં એક ઉપકરણને વિદ્યુતપ્રવાહ પહોંચાડવામાં થાય છે.કોષોને કેવી રીતે જોડાવા જોઈએે કે જેથી અવરોધને પાવર ન્યૂનત્તમ સંખ્યામાં કોષનો ઉપયોગ કરીને પહોંચાડી શકાય ?View Solution
