કેપ્લરનો બીજો નિયમ કયા નિયમનું વિધાન છે
Easy
c
Considering a small area swept by a planet in time dt is, \(d A=\frac{1}{2} r \cdot(r d \theta)\)
Considering a small area swept by a planet in time dt is, \(d A=\frac{1}{2} r \cdot(r d \theta)\)
\(\therefore\) So, rate of swept of area.
\(\frac{d A}{d t}=\frac{1}{2} r\left(r \frac{d \theta}{d t}\right)\)
We know angular momentum, \(\vec{L}=m r^2 \frac{d \vec{\theta}}{d t}\)
So, \(\frac{d A}{d t}=\frac{1}{2 m}\left(m r^2 \frac{d \theta}{d t}\right)=\frac{L}{2 m}\)
Now, a planet sweeps equal amount of area in same time interval of its revohution. (from 2 nd law) So, \(\frac{d A}{d t}=\) constant; Hence \(L\) is also constant
\(\therefore\) The \(2^{nd}\) law is nothing but a shatement of conservation of angular momentum.
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1પૃથ્વીની સપાટીથી $4{R_e}$ ઊંચાઇ પર રહેલા $m$ દળના પદાર્થની નિષ્ક્રમણ ઊર્જા કેટલી થાય? ($R$= પૃથ્વીની ત્રિજયા)View Solution
- 2એક $m$ દળનો ઉપગ્રહ $A$ પૃથ્વીના કેન્દ્રથી $r$ અંતરે છે. બીજો $2m$ દળનો ઉપગ્રહ $B$ પૃથ્વીના કેન્દ્રથી $2r$ અંતરે છે. તેમના આવર્તકાળનો ગુણોત્તર કેટલો થાય?View Solution
- 3એક નવા ગ્રહનો વિચાર કરો, જેની ઘનતા પૃથ્વીની ઘનતા જેટલી છે, પરંતુ તેનો આકાર પૃથ્વી કરતાં ત્રણ ગણો મોટો છે. જો પૃથ્વીની સપાટી પર ગુરુત્વાકર્ષણને કારણે પ્રવેગ $g$ છે, તો નવા ગ્રહની સપાટી પર $g'$ હોય, તોView Solution
- 4View Solutionગુરુત્વાકર્ષણ અચળાંક એ શેના પર આધાર રાખે છે ?
- 5બે ઉપગ્રહો $A$ અને $B$ ના દળો અનુક્રમે $m$ અને $2 m$ છે. પૃથ્વીને ફરતે, $A$ એ $R$ ત્રિજ્યાની વર્તુળાકાર કક્ષા અને $B$ એ $2R$ ત્રિજ્યાની વર્તુળાકાર કક્ષામાં છે. તેની ગતિ ઊર્જાઓનો ગુણોત્તર $K.E._A / K.E._B ,$ કેટલો થાય?View Solution
- 6View Solutionસૂર્યની ફરતે ભ્રમણ કરતાં ગ્રહ માટે નીચેના માથી ક્યો ગ્રાફ સાચો છે ?
- 7પૃથ્વી પર પદાર્થની નિષ્ક્રમણ ઝડપ $V_e $ છે . તો ગ્રહ જેનું દળ પૃથ્વીના દળ કરતાં બમણું અને ત્રિજ્યા પૃથ્વીની ત્રિજ્યા કરતાં $3$ ગણી હોય તો તે ગ્રહ પર પદાર્થની નિષ્ક્રમણ ઝડપ કેટલી થાય?View Solution
- 8સ્પેશશીપનું દળ $1000$ $kg$ છે. તેને પૃથ્વીની સપાટીથી શૂન્યાવકાશમાં છોડવામાં આવે છે. $‘g’$ અને $‘R’$ ની કિંમત અનુક્રમે $10$ $m/s^2$ અને $6400$ $km$ છે. તો આ કાર્ય કરવા કેટલી ઊર્જાની જરૂર પડે?View Solution
- 9$R$ પૃથ્વીની ત્રિજયા અને $\omega $ કોણીય ઝડપ છે.ઘ્રુવપ્રદેશ પાસે ગુરુત્વપ્રવેગનું મૂલ્ય $g_p$ છે.તો $60^o$ અંક્ષાશ પર ગુરુત્વપ્રવેગનું મૂલ્ય કેટલું થાય?View Solution
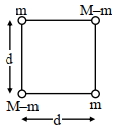
- 10$2 {M}$ દળના પદાર્થને ચાર $\{{m}, {M}-{m}, {m}, {M}-{m}\}$ દળના ટુકડામાં વિભાજિત કરીને આકૃતિમાં દર્શાવ્યા પ્રમાણે ચોરસમાં ગોઠવેલા છે. જ્યારે ગુરુત્વાકર્ષી સ્થિતિઉર્જા મહતમ હોય ત્યારે $\frac{{M}}{{m}}$ નો ગુણોત્તર ${x}: 1$ મળતો હોય તો $x$ નું મૂલ્ય કેટલું કેટલું હશે?View Solution