किसी खगोलीय दूरबीन के अभिदृश्यक और नेत्रिका की फोक्स दूरियां कमश: $40$ से.मी. और $4$ से.मी. हैं। अभिदृश्यक से $200$ से.मी. दूर स्थित किसी बिम्ब को देखने के लिए दोनों लेंसों के बीच की दूरी होनी चाडिए:
[2016]
Download our app for free and get started
दिया है, वस्तु लोन्स की फोकस दूरी $f _0=40 \ cm$
नेत्रिका की फोकस दूरी $f_e=4 \ cm$
प्रतिबिम्ब की दूरी, $v _0=200 \ cm$
वस्तु लेंस के लिए लोंस के सूत्र से,
$ \frac{1}{v_0}-\frac{1}{ u _0}=\frac{1}{ f _0}$
$\Rightarrow \frac{1}{ v _0}=\frac{1}{ f _0}+\frac{1}{ u _0}$
$\Rightarrow \frac{1}{ v _0}=\frac{1}{40}+\frac{1}{-200}=\frac{+5-1}{200}$
$\Rightarrow v _0=50 \ cm $
नली की लंबाई $\ell=\left| v _0\right|+ f _{ e }=50+4=54 \ cm$.
नेत्रिका की फोकस दूरी $f_e=4 \ cm$
प्रतिबिम्ब की दूरी, $v _0=200 \ cm$
वस्तु लेंस के लिए लोंस के सूत्र से,
$ \frac{1}{v_0}-\frac{1}{ u _0}=\frac{1}{ f _0}$
$\Rightarrow \frac{1}{ v _0}=\frac{1}{ f _0}+\frac{1}{ u _0}$
$\Rightarrow \frac{1}{ v _0}=\frac{1}{40}+\frac{1}{-200}=\frac{+5-1}{200}$
$\Rightarrow v _0=50 \ cm $
नली की लंबाई $\ell=\left| v _0\right|+ f _{ e }=50+4=54 \ cm$.
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$f _1$ और $f _2$ फोकस दूरियों के दो पतले लैंस अक्षीय रूप से जुड़े हुए हैं। इस युग्म की शक्ति (पावर) होगी :View Solution
- 2एक प्रिज्म जिसका कोण $A$ है, के एक समतल पर एक किरण आपतन कोण बनाते हुए आती है तथा वह दूसरे समतल के लम्बवत बाहर निकलती है। यदि प्रिज्म के पदार्थ का अपवर्तनांक $\mu$ हो तो आपतन कोण $i$ का मान लगभग होगा:View Solution
- 3विचलन कोण $\delta$, अपवर्तनांक $\mu$ तथा प्रिज्म कोण $A$ है तो निम्न में से कौन सा कथन सत्य है?View Solution
- 4View Solutionकिन विमाओं के लिए किरण प्रकाशिकी लागु होता है?
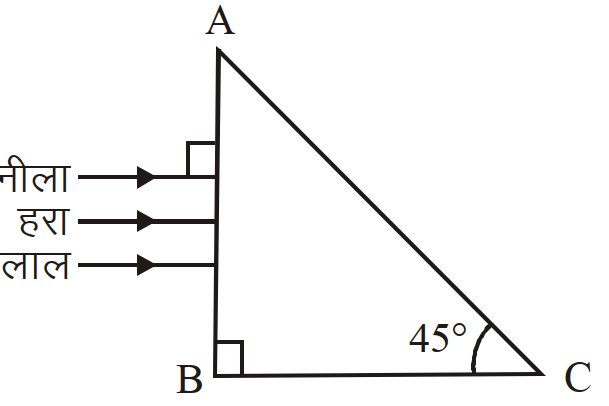
- 5एक प्रकाश किरणपूंज, लाल, हरे तथा नीले रंगों से बना है। यड किरणपुंज किसी समकोणी प्रिज्म पर आपतित होता है $($ आरेख देखिये $)$ प्रिज्म के पदार्थ का अपवर्तनांक, लाल, हरे, व नीले रंग के लिये क्रमश: $1.39$, $1.44$ तथा $1.47$ है, तो यह प्रिज्म:View Solution
- 6सामान्य नेत्त्र में कौर्निया $($स्वच्छ मंडल$)$ की अभिसारी शक्ति $40 D$ है तथा कार्निया के पीछे नेत्र लेंस की न्यूनतम अभिसारी शक्ति $20 D$ है। इस सूचना से नेत्र के रेटिना $($दृष्टिपटल$)$ तथा लेन्स के बीच की अनुमानित दूरी होगी:View Solution
- 7View Solutionउत्तल लैस की फोकस दूरी उच्चतम होगी
- 8प्रिज्म के पदार्थ का अपवर्तनांक $\sqrt{2}$ तथा इसका अपवर्तन कोण $30^{\circ}$ है। प्रिज्म के अपवर्तक पृष्ठों में से किसी एक पृष्ठ को अन्दर की ओर दर्पणनुमा बनाया जाता है। दूसरे पृष्ठ पर आपतित एकवर्णी प्रकाश पुँज दर्पण से परावर्तित होकर अपने ही मार्ग से वापिस लौट आएगा यदि प्रिज्म पर आपतन कोण है:View Solution
- 9प्रिज्म के पदार्थ का अपवर्तनांक $\sqrt{3}$ है। न्यूनतम विचलन कोण का मान होगा :View Solution
- 10कोई लड़का कागज़ पर एक समउत्तल लैंस द्वारा सूर्य किरणों को फोकस कर आग जलाना चाहता है। लैंस की फोकस दूरी $10 cm$ है। सूर्य का व्यास $1.39 \times 10^9 m$ है और इसकी पृथ्वी से मध्यमान दूरी $1.5 \times 10^{11} m$ है। सूर्य के कागज़ पर प्रतिबिम्ब का व्यास होगा:View Solution