$L = 2\,mH$ ઇન્ડકટરમાંથી પસાર થતો પ્રવાહ સમય સાથે $i = t^2e^{-t}$ મુજબ બદલાય છે. કેટલા સમયે ($sec$ માં) $e.m.f.$ શૂન્ય થાય?
AIPMT 2001, Medium
Download our app for free and get started
c
\(\mathrm{L}=2 \mathrm{\,mH}, \mathrm{i}=\mathrm{t}^{2} \mathrm{e}^{-t}\)
\(\mathrm{L}=2 \mathrm{\,mH}, \mathrm{i}=\mathrm{t}^{2} \mathrm{e}^{-t}\)
\(\mathrm{E}=-\mathrm{L} \frac{\mathrm{di}}{\mathrm{dt}}=-\mathrm{L}\left[-\mathrm{t}^{2} \mathrm{e}^{-\mathrm{t}}+2 \mathrm{te}^{-\mathrm{t}}\right]\)
when \(E=0\)
\(-\mathrm{e}^{-\mathrm{t}} \mathrm{t}^{2}+2 \mathrm{te}^{-\mathrm{t}}=0\)
\(2 t e^{-t}=e^{-t} t^{2}\)
\(t=2 \sec\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
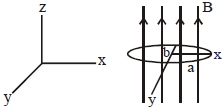
- 1$R$ અવરોધ ધરાવતી ઉપવલય લૂપની અર્ધદીર્ધ અક્ષ $a$ અને અર્ધલઘુ અક્ષ $b$ ને ચુબકીયક્ષેત્રમાં મૂકેલી છે. જો લૂપને $x-$ અક્ષને અનુલક્ષી ને $\omega$ કોણીય આવૃતિથી ભ્રમણ કરાવતા જુલ અસરના કારણે લૂપમાં પાવર વ્યયView Solution
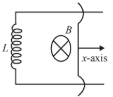
- 2આકૃતિમાં દર્શાવ્યા પ્રમાણે એક $L$ આત્મપ્રેરકત્વ ધરાવતું ગુચળું બે પાટા સાથે જોડાયેલ છે. આ બે સમાંતર પાટા પર એક $l$ લંબાઈ અને $m$ દળ ધરાવતું કનેક્ટર મુક્ત રીતે લસરી શકે છે. આ આખા તંત્રને કાગળના સમતલની અંદરની દિશામાં જતાં ચુંબકીયક્ષેત્ર $B$ માં મૂકવામાં આવે છે. $t= 0$ સમયે તેને શરૂઆતનો વેગ $v_0$ આપેલ છે જેના કારણે તે $x-$દિશામાં ગતિ કરવાનું શરૂ કરે છે.તો કનેક્ટરના સ્થાનતરનો સમય વિરુદ્ધનો આલેખ કેવો મળશે?View Solution
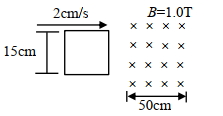
- 3$15$ $cm$ની બાજુ ધરાવતા એક ચોરસ ગાળાને આાકૃત્તિમાં દર્શાવ્યા અનુસાર $2 \mathrm{~cm} / \mathrm{s}$ની અચળ ઝડપથી જમણીબાજુ ગતિ કરાવવામાં આવે છે. તેની આગળની ધાર (બાજુ) 50 $\mathrm{cm}$ પહોળા (ફેલાયેલા) યુંબકીયક્ષેત્રમાં $t=0$ સમયે દાખલ થાય છે. ગાળામાં $t=10 \mathrm{~s}$ એ પ્રરિત emfનું મૂલ્ય.......... થશે.View Solution
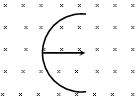
- 4$L$ લંબાઇના તારને અર્ધવર્તુળાકારમાં વાળીને $v$ વેગથી ગતિ કરાવતાં તેનાં બે છેડા વચ્ચે કેટલો $emf$ ઉત્પન્ન થાય?View Solution
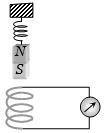
- 5View Solutionઆપેલ આકૃતિમાં જ્યારે ચુંબક દોલનો કરે ત્યારે..
- 6$2.0\,cm$ બાજુ ધરાવતી ચોરસ લૂપને પ્રતિ સે.મી.$50$ આંટા, $2.5\,A$ કંપવિસ્તારના સાઈન પ્રકાર બદલાતા પ્રવાહ ધારિત અને $700\,rad\, s ^{-1}$ કોણીય આવૃત્તિવાળા સોલેનોઇડની અંદર મુકેલ છે. લૂપની કેન્દ્રીય અક્ષ અને સોલેનોઈડની અક્ષ સંપાત થાય છે. લૂપમાં ઉત્પન્ન થતા $emf$ નો કંપવિસ્તાર $x \times 10^{-4}\,V$ છે.તો $x$ નું મૂલ્ય ...... છે. $\pi=\frac{22}{7}$ લો.)View Solution
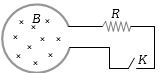
- 7ચુંબકીયક્ષેત્રનો ફેરફાર $B = {B_0}{e^{ - t}}$ મુજબ થાય છે,કોઇલની ત્રિજયા $r$ અને અવરોધ $R$ છે.તો કળ ($K$) બંધ કરતાં કેટલો પાવર ઉત્પન્ન થાય?View Solution
- 8કોઇલ સાથે સંકળાયેલ ફલકસ $\phi \, = \,10{t^2}\, - \,50t\, + 250$ હોય તો $t = 3\,s$ સમયે ઉદભવતું $e.m.f = .......$View Solution
- 9ટ્રાન્સફોર્મરમાં પ્રાથમિક અને ગૌણ ગૂંચળા વચ્ચે અનોન્યપ્રેરકત્વ $0.2\, H$ છે,પ્રાથમિક ગૂંચળામાં પ્રવાહ $5 \,A /Sec$ નો ફેરફાર કરતાં ગૌણ ગૂંચળામાં કેટલો $emf$ .........$V$ ઉત્પન્ન થાય?View Solution
- 10View Solutionએક ગુંચળાંને સમય સાથે બદલાતા ચુંબકીય ક્ષેત્રમાં રાખેલ છે. એ ગૂંચળામાં આંટાની સંખ્યા અડધી અને તારની ત્રિજ્યા બમણી કરવામાં આવે તો, ગૂંચળાંમાં પ્રેરિત પ્રવાહને કારણે વિખેરાતી વિદ્યુતીય કાર્યત્વરા (પાવર)............. હશે. (એવું ઘારો કે ગૂંચળાંને લધુપથિત કરેલ છે.)