$l$ લંબાઈ અને $M$ દળનો એક સળિયો તેના બે છેડામાંથી પસાર થતી સમક્ષિતિજ અક્ષને અનુલક્ષીને આંદોલનો કરે છે. તેનો મહત્તમ કોણીય વેગ $\omega$ છે. તો આ સળિયાનું દ્રવ્યમાન કેન્દ્ર મહત્તમ કેટલી ઊંંચાઈ પ્રાપ્ત કરે?
AIEEE 2009, Medium
d
The moment of inertia of the rod about \(O\) is
The moment of inertia of the rod about \(O\) is
\(\frac{1}{3}m{\ell ^2}\). The maximum angular speed of the rod is when the rod is instantaneously vertical. The energy of the rod in this condition is \(\frac{1}{2}I{\omega ^2}\,\) where \(I\) is the moment of inertia of the rod about \(O.\) When the rod is in extreme portion, its angular velocity is zero momentarily. In this case, the energy of the rod is mgh where h is the maximum height to which the center of mass \((C.M)\) rises
\(\begin{array}{l}
\therefore \,mgh = \frac{1}{2}I{\omega ^2} = \frac{1}{2}\left( {\frac{1}{3}m{l^2}} \right){\omega ^2}\\
\Rightarrow h = \frac{{{\ell ^2}{\omega ^2}}}{{6g}}
\end{array}\)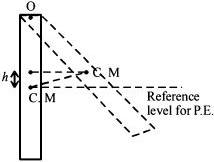
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક બળ $\vec{F}=(2 \hat{i}+3 \hat{j}-5 \hat{k}) \,N$ બિંદુ $\vec{r}_1=(2 \hat{i}+4 \hat{j}+7 \hat{k}) \,m$. ઉપર લાગુ કરવામાં આવે છે. તો બિંદુ $\vec{r}_2=(\hat{i}+2 \hat{j}+3 \hat{k}) \,m$ ને અનુલક્ષીને બળ વડે ઉદભવતું ટોર્ક ............ $Nm$ હશે ?View Solution
- 2બે સમાન નળાકારમાંનો એક નળાકાર $-A \,\,50$ પરિભ્રમણ પ્રતિ સેકન્ડની કોણીય ઝડપે ગતિ કરે છે. ગતિ કરતો આ નળાકાર બીજા સ્થિર નળાકાર $- B $ ના સંપર્કમાં લાવવામાં આવે છે. બંને નળાકાર વચ્ચે ગતિક ઘર્ષણના કારણે સ્થિર નળાકાર સ્થિર સ્થિતિમાંથી કોણીય પ્રવેગથી ચાકગતિ શરૂ કરે છે. જ્યારે નળાકાર $-A $ પ્રતિપ્રવેગથી ચાકગતિ કરે છે. જો બંને નળાકારના કોણીય પ્રવેગનાં માનાંક $1$ પરિભ્રમણ પ્રતિ સેકન્ડ હોય, તો ...... $(\sec)$ સમય બાદ બંને નળાકારની કોણીય ઝડપ સમાન થાય.View Solution
- 3$m_1$ અને $m_2$ $(m_1 > m_2)$ દળના બે કણો સ્થિર સ્થિતિમાથી શરૂ કરીને એકબીજા તરફ આકર્ષીબળ ના વ્યસ્ત વર્ગના નિયમ મુજબ ગતિ કરે છે. આ તંત્ર માટે દ્રવ્યમાન $(CM)$ કેન્દ્ર માટે નીચેનામાથી સાચું વિધાન પસંદ કરો.View Solution
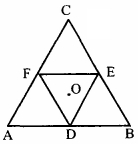
- 4એક પાતળી લાકડાની ઘન તક્તિમાંથી $ABC$ સમબાજુ ત્રિકોણ બનાવવામાં આવે છે (આકૃતિ જુઓ). $D, E$ અને $F$ એ આકૃતિમાં દર્શાવ્યા મુજબ તેની બાજુના મધ્યબિંદુઓ છે અને $G$ એ ત્રિકોણનું કેન્દ્ર છે. ત્રિકોણના સમતલને લંબ અને $G$ માંથી પસાર થતી અક્ષને અનુલક્ષીને ત્રિકોણની જડત્વની ચાકમાત્રા $I_o$ છે. જો $ABC$ માંથી નાનો ત્રિકોણ $DEF$ કાઢી નાખવામાં આવે તો બાકી રહેલ આકૃતિ માટે આ જ અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા $I$ થતી હોય તોView Solution
- 5ચક્ર તેની અક્ષને અનુલક્ષીને ચાકગતિ કરે છે. અક્ષ પર ઘર્ષણના કારણે તેનો કોણીય પ્રતિપ્રવેગ તેના કોણીય વેગના સમપ્રમાણ છે. $n$ પરિભ્રમણમાં તેનો કોણીય વેગ અડધો થાય, તો તે વધારાના કેટલા પરિભ્રમણ કરીને સ્થિર થશે?View Solution
- 6$M$ દળના એક પદાર્થને એક ઘર્ષણરહિત બેરીંગ ઉપર રાખેલી ગરગડી પર વીંટાળેલી દોરી વડે લટકાવવામાં આવે છે. ગરગડીનું દળ $m$ અને ત્રિજ્યા $R$ છે. તો પદાર્થનો પ્રવેગ કેટલો હશે?View Solution
ગરગડીને વર્તુળાકાર તકતી ધારો તથા દોરી એ ગરગડી પર સરકતી નથી એમ ધારો.
- 7પૃષ્ઠને લંબ એવા કેન્દ્રમાંથી પસાર થતી અક્ષને અનુલક્ષીને $I_{1}$ જેટલી જડત્વની ચાકમાત્રા ધરાવતી તકતી આ અક્ષને અનુલક્ષીને $\omega$ જેટલા કોણીય વેગથી ભ્રમણ કરે છે.હવે,પૃષ્ઠને લંબ એવા કેન્દ્રમાંથી પસાર થતી અક્ષને અનુલક્ષીને $I_{2}$ જેટલી જડત્વની ચાકમાત્રા ધરાવતી બીજી તકતી પર મૂકવામાં આવે, તો આ બંને તકતીનો સંયુકત કોણીય વેગ કેટલો હશે?View Solution
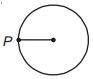
- 8$m$ દળ અને $R$ ત્રિજ્યા વાળી એક નિયમિત તક્તીને $P$ બિંદુ પર કિલકિત કરેલી છે અને તે શિરોલંબ સમતલમાં મુક્ત રીતે ભ્રમણ કરે છે.શરૂઆતમાં તકતીનો કેન્દ્ર $C$ એ $P$ સાથે સમક્ષિતિજ સ્થિતિમાં છે. જો તેને આ સ્થિતિ પરથી મુક્ત કરવામાં આવે, તો જ્યારે રેખા $PC$ એ સમક્ષિતિજ સાથે $\theta$ ખૂણો બનાવે ત્યારે તેનો કોણીય પ્રવેગ શું હશે ?View Solution
- 9એક પદાર્થ માત્ર કોણીય ગતિ કરે છે જો કણ નો રેખીય વેગ $v$ અને તે $x$-અક્ષ થી $r$ અંતરે $\omega $ કોણીય વેગ થી ફરતો હોય $\omega = \frac{v}{r}$ હોય તો પદાર્થ માટે શું સાચું છે ?View Solution
- 10ઘર્ષણ રહિત પુલીને વીટાળેલા દોરીના છેડે દળ લટકાવેલ છે. પુલીનું દળ $ m $ અને ત્રિજ્યા $ R$ છે. પુલી એ નિયમિત વર્તૂળાકાર તકતી હોય અને દોરા પુલી સર સરકતી ના હોય, તો દળનો પ્રવેગ .......View Solution
