$l $ લંબાઇની દોરીના એક છેડે $m$ દળના કણ અને બીજા છેડાને સમક્ષિતિજ સમતલ ટેબલ પર રહેલ નાની ખીલી સાથે બાંધેલ છે. જો કણ $v$ ઝડપથી વર્તુળમાં ગતિ કરે, તો તેના પર લાગતું કુલ બળ (કેન્દ્ર તરફ) કેટલું હશે? ($T$ દોરડા પરનું તણાવ છે)
NEET 2017, Easy
Download our app for free and get started
c
Centripetal force \(\frac{mv^2}{l}\) is provided by tension so net force on the particle will be equal to tension \(T\)
Centripetal force \(\frac{mv^2}{l}\) is provided by tension so net force on the particle will be equal to tension \(T\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$L$ લંબાઇની ચેઇનને ટેબલ પર મૂકેલ છે.તેમાંથી લટકાવી શકાતી મહત્તમ લંબાઇ $l$ હોય,તો ચેઇન અને ટેબલ વચ્ચેનો ઘર્ષણાંક કેટલો થાય?View Solution
- 2View Solutionજ્યારે ઢાળ પર રહેલો પદાર્થ ગતિ ના કરે તો ઘર્ષણબળ ...
- 3View Solutionમર્યાદિત ઘર્ષણ એ
- 4$2\,kg$ દળનો કોઈ પદાર્થ $3\,m/s^2$ ના પ્રવેગ થી $30^o$ ઢોળાવવાળા ખરબચડા સમતલ પર સરકે છે.તો પદાર્થને તે જ સમતલ પર તેટલા જ પ્રવેગથી ઉપર ચડાવવા માટે જરૂરી બાહ્ય બળ ........ $N$ થશે. $(g\, = 10\, m/s^2)$View Solution
- 5View Solutionનીચેના માથી કયું વિધાન સાચું છે?
- 6View Solutionસંપર્કમાંની બે વસ્તુઓ વચ્ચેનું સીમાંત મર્યાદિત ઘર્ષણ એ શેનાથી સ્વતંત્ર છે
- 7$30^{\circ}$ સમક્ષિતિજ સાથે ખૂણો ધરાવતા ઢાળ પર ઉપર તરફ $10\, {ms}^{-2}$ ના પ્રવેગથી એક કાર ગતિ કરે છે. કારની છત પર દોરી બાંધી તેના છેડે લોકલ લટકાવેલ છે. તો દોરીએ શિરોલંબ સાથે બનાવેલ ખૂણો કેટલો હશે? (${g}=10\, {ms}^{-2}$ )View Solution
- 8$30^{\circ}$ ખૂણે રહેલ ઢાળ પર એક બ્લોક ઉપર તરફ $v_{0}$ જેટલા શરૂઆતના વેગથી ગતિ કરે છે. તે પોતાના મૂળ સ્થાને ફરીથી $\frac{v_{0}}{2}$ જેટલા વેગથી પાછો આવે છે. બ્લોક અને ઢાળ વચ્ચેના ગતિક ઘર્ષણાંકનું મૂલ્ય લગભગ $\frac{ I }{1000}$ હોય તો $I$ નું પૂર્ણાંકમાં મૂલ્ય લગભગ કેટલું હશે?View Solution
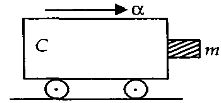
- 9આકૃતિમાં દર્શાવ્યા મુજબ એક $m $ દળનો બ્લોક એક ગાડા $C$ સાથે સંપર્કમાં છે. બ્લોક અને ગાડા વચ્ચેનો સ્થિતિ ઘર્ષણાંક $\mu $ છે. બ્લોકને પડતો અટકાવવા માટે ગાડાનો પ્રવેગ $\alpha $ કેટલો હોવો જોઇએ?View Solution
- 10$50\, kg$ નો બ્લોક રફ સપાટી પર પડેલ છે.બ્લોક અને સપાટી વચ્ચેનો ઘર્ષણાંક $0.6$ છે.શિરોલંબ સાથે $30^°$ ખૂણે ...... $N$ લઘુત્તમ બળ લગાવવું જોઈએ કે જેથી બ્લોક માત્ર ગતિ કરવાનું શરૂ કરે.View Solution