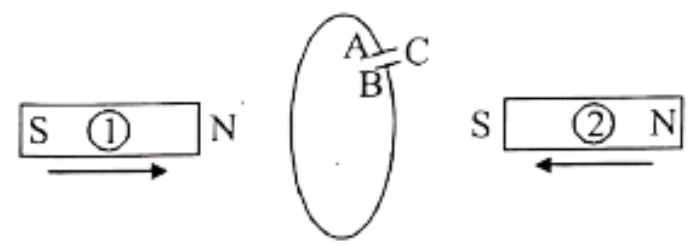
$L_1$ व $L_2$ स्वप्रेरकत्व वाली कुण्डलियों के मध्य महत्तम अन्योन्य प्रेरकत्व क्या होगा$?$
Download our app for free and get started
जब एक कुण्डली पर दूसरी कुण्डली को लपेटा जाता है तो दोनों कुण्डलियों के पूर्ण रूप से युग्मित होने के कारण अन्योन्य प्रेरण गुणांक का मान अधिकतम होता है। फलस्वरूप प्रेरित वि.वा. बल का मान भी अधिकतम होता है।
जब दोनों कुण्डलियों को किसी अन्य प्रकार से लपेटने पर अन्योन्य प्रेरण गुणांक व प्रेरित वि.वा. बल अधिकतम नहीं हो पाते क्योंकि दोनों कुण्डलियों में फ्लक्स की सम्बद्धता पूर्ण रूप से नहीं होती है।
दो कुण्डली जिनके प्रेरकत्व $L _1$ तथा $L _2$ हैं और उनका अन्योन्य प्रेरण $M$ है। तब $L_1, L_2$ और $M$ में सम्बन्ध
$M=K \sqrt{L_1 L_2}$
जहाँ $K$ कुण्डलियों $($परिनालिकाओं$)$ का युग्मन गुणांक है। आदर्श स्थिति में $K = 1$
इसलिये $M$ का अधिकतम मान $\sqrt{ L _1 L_2}$होगा।
जब दोनों कुण्डलियों को किसी अन्य प्रकार से लपेटने पर अन्योन्य प्रेरण गुणांक व प्रेरित वि.वा. बल अधिकतम नहीं हो पाते क्योंकि दोनों कुण्डलियों में फ्लक्स की सम्बद्धता पूर्ण रूप से नहीं होती है।
दो कुण्डली जिनके प्रेरकत्व $L _1$ तथा $L _2$ हैं और उनका अन्योन्य प्रेरण $M$ है। तब $L_1, L_2$ और $M$ में सम्बन्ध
$M=K \sqrt{L_1 L_2}$
जहाँ $K$ कुण्डलियों $($परिनालिकाओं$)$ का युग्मन गुणांक है। आदर्श स्थिति में $K = 1$
इसलिये $M$ का अधिकतम मान $\sqrt{ L _1 L_2}$होगा।
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionगतिक विद्युत वाहक बल के व्यंजक की स्थापना कीजिये।
- 2View Solutionविधुत-चुम्बकीय प्रेरण के फैराडे के नियम लिखिये और उन्हें व्युत्पन्न कीजिये।
- 3View Solutionअन्योन्य प्रेरकत्व की परिभाषा और इसका SI मात्रक लिखिए।
- 4विद्युतचुम्बकीय प्रेरण के लेंज नियम का कथन लिखिए।View Solution
पूर्व से पश्चिम दिशा में स्थित कोई 2 मी. लम्बा सीधा क्षैतिज चालक तार $0.3 \times 10^{-4}$टेसला के पृथ्वी के चुम्बकीय क्षेत्र के क्षैतिज घटक के लम्बवत 5 मी/से की चाल से गिर रहा है। तार के सिरों के मध्य प्रेरित विद्युत वाहक बल के तात्क्षणिक मान की गणना कीजिए। - 5यदि । लम्बाई की धात्विक छड़ को एक समान चुम्बकीय क्षेत्रअ (B) के लम्बवत् रखकर इसे चुम्बकीय क्षेत्र के लम्बवत $v$ वेग से चलाएँ तो इसके सिरों के बीच प्रेरित विद्युत वाहक बल (गतिक विद्युत वाहक बल) ज्ञात कीजिए। आवष्यक चित्र बनाइए।View Solution
- 6View Solutionसमरूप चुम्बकीय क्षेत्र में चकती की घूर्णन गति के कारण उत्पन्न प्रेरित वि.वा. बल के व्यंजक की स्थापना कीजिये।
- 7View Solution
- 8(i) लेंज का नियम ऊर्जा संरक्षण सिद्धान्त का निष्कर्ष है, इसको कैसे दर्शाएँगे? उचित उदाहरण सहित व्याख्या कीजिए।View Solution
(ii) किसी चालक के आवेश वाहकों पर कार्यरत लॉरेन्ट्ज बल के व्यंजक का उपयोग उस प्रेरित विद्युत्-वाहक बल (emf), जो किसी चुम्बकीय क्षेत्र B के लम्बवत् । लम्बाई के चालक को वेग $v$ से गति करने पर चालक में उत्पन्न होता है, के लिए व्यंजक प्राप्त करने में कीजिए। - 9View Solutionविद्युत चुम्बकीय प्रेरण सम्बन्धी लेन्ज का नियम क्या है? इससे ऊर्जा संरक्षण के नियम की अनुपालना किस प्रकार होती है? समझाइये।
- 10View Solutionचुम्बकीय फ्लक्स क्या है? इसकी निर्भरता कारों को समझाइये।
