$LR$ શ્રેણી પરિપથને $\omega $ આવૃતિ ધરાવતા $AC$ સ્ત્રોત સાથે જોડેલ છે જેનો ઇન્ડક્ટિવ રીએક્ટન્સ $2R$ છે. હવે $R$ કેપેસિટીવ રીએક્ટન્સ ધરાવતા કેપેસીટરને $L$ અને $R$ સાથે શ્રેણીમાં જોડેલ છે. તો નવા અને જૂના પાવર ફેકટરનો ગુણોત્તર શું મળે?
JEE MAIN 2013, Diffcult
d
Power factor \(_{(old)}\)
Power factor \(_{(old)}\)
\(=\frac{\mathrm{R}}{\sqrt{\mathrm{R}^{2}+\mathrm{X}_{\mathrm{L}}^{2}}}=\frac{\mathrm{R}}{\sqrt{\mathrm{R}^{2}+(2 \mathrm{R})^{2}}}=\frac{\mathrm{R}}{\sqrt{5 \mathrm{R}}}\)
Power factor \(_{(\text {new })}\)
\(=\frac{\mathrm{R}}{\sqrt{\mathrm{R}^{2}+\left(\mathrm{X}_{\mathrm{L}}-\mathrm{X}_{\mathrm{C}}\right)^{2}}}=\frac{\mathrm{R}}{\sqrt{\mathrm{R}^{2}+(2 \mathrm{R}-\mathrm{R})^{2}}}\)
\(=\frac{\mathrm{R}}{\sqrt{2} \mathrm{R}}\)
\(\therefore\) \(\frac{{New\,power\,factor}}{{Old\,power\,factor}} = \frac{{\frac{{\text{R}}}{{\sqrt {{\text{2R}}} }}}}{{\frac{{\text{R}}}{{\sqrt {5{\text{R}}} }}}} = \sqrt {\frac{5}{2}} \)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક $200\, V , 50 \,Hz$ ના $ac$ સપ્લાય સાથે $40\, \mu F$ નો એક કેપેસીટર જોડેલ છે આ પરિપથમાના પ્રવાહનું $rms$ મુલ્ય આશરે .......................$\;A$ છેView Solution
- 2એક ગૂંચળાનું $ 50\;Hz$ આવૃતિએ અવરોઘ $30$ ઓહ્મ અને ઇન્ડકિટવ રિએકટન્સ $20$ ઓહ્મ છે. જો ગૂંચળાના બે છેડાને $200\;V,100\;Hz $ ના $ac$ ઉદ્ગમ સાથે જોડવામાં આવે, તો ગૂંચળામાંથી વહેતો પ્રવાહ ($A$ માં) કેટલો હશે?View Solution
- 3એક વૈકલ્પિક ઈએમએફનું પ્રતિરોધ $R$, કેપેસીિટન્સ $ C $ અને ઇન્ડક્ટન્સ $ L $ ના સમાંતર સંયોજનમાં લાગુ કરવામાં આવે છે. જો $ I_R $, $ I_L $, $ I_C $ અનુક્રમે $ R, \, L $ અને $ C$ દ્વારા પ્રવાહો હોય, તો પછી ચિત્ર જે યોગ્ય રીતે રજૂ કરે છે, $ I_R $, $ I_L $, $ I_C$ વચ્ચેના તબક્કાના સંબંધો અને સ્રોત ઇએમએફ $E$ દ્વારા આપવામાં આવે છેView Solution
- 4$RL$ પરિપથનો પાવર ફેકટર $1/2$ છે.જો $R = 100\,\Omega $ હોય,તો $L$ કેટલો થાય ? $ac$ની આવૃત્તિ $50 \,Hz$ છે.View Solution
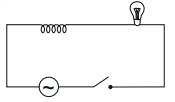
- 5આકૃતિમાં દર્શાવ્યા મુજબ એક પ્રકાશનો બલ્બ અને એક ઇન્ડકટર કોઇલને કળ વડે $AC$ પ્રવાહ સાથે જોડવામાં આવે છે જ્યારે કળ બંધ કરવામાં આવે અને થોડાક સમય બાદ એક લોખંડના સળિયાને ઇન્ડકટર કોઇલમાં દાખલ કરવામાં આવે ત્યારે પ્રકાશના બલ્બની તીવ્રતા .....................View Solution
- 6એક $ L-C-R$ પરિપથમાં અવરોધ, કેપેસિટન્સ અને ઇન્ડકટરની આસપાસ વિદ્યુતસ્થિતિમાનનો તફાવત અનુક્રમે $80\;V,40\;V $ અને $100\;V$ છે. પરિપથનો પાવર ફેકટર કેટલો હશે?View Solution
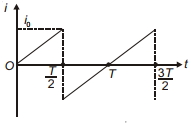
- 7View Solutionઆલેખ વડે દર્શાવેલ વિદ્યુતપ્રવાહ ફેરફાર માટે અર્ધચક્ર માટે વિદ્યુતપ્રવાહના મૂલ્યનો સરેરાશ કેટલો છે ?
- 8એક શ્રેણી $L.R$ પરિપથને $E=25 \sin 1000 t V$ ના $AC$ ઉદ્દગમ સાથે જોડેલ છે અને તેનો પૉવર ફેકટર $\frac{1}{\sqrt{2}}$ છે. જો ઉદ્દગમ નું $emf$ બદલાઈને $\mathrm{E}=20 \sin 2000 \mathrm{tV}$ થાય તો પરિપથમાં નવો પૉવર ફેક્ટર_________થશે.View Solution
- 9$ac$ પરિપથમાં પ્રત્યાવર્તી વોલ્ટેજ, $e=200 \sqrt{2} \sin 100 t$ વોલ્ટને $1 \;\mu F$ના કેપેસીટન્સ ધરાવતા કેપેસિટર સાથે જોડેલ છે. આ પરિપથમાં પ્રવાહનું $rms$ મૂલ્ય ($mA$ માં) કેટલું હશે?View Solution
- 10$10 \sqrt{3}\; \Omega$ અવરોધ, $40\; \Omega$ કેપેસિટિવ રિએકટન્સ અને $30 \Omega$ ઈન્ડકટિવ રિએકટન્સના શ્રેણી પરિપથમાં $220\,V$ નો ઓલ્ટરનેટિંગ વિદ્યુતસ્થિતિમાન લગાવેલ છે. શૂન્ય અને અનંત આવૃત્તિ માટે પરિપથમાં વિદ્યુતપ્રવાહ અનુક્રમે કટલો છે?View Solution
