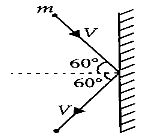
$m$ દળનો દઢ દડો કોઇ દઢ દીવાલ સાથે નીચે દર્શાવેલ આકૃતિ અનુસાર $60^o$ ના ખૂણે અથડાઇને ઝડપ ગુમાવ્યા વગર પરાવર્તન પામે છે. દીવાલ વડે દડા પર કેટલો આઘાત લાગશે?

NEET 2016, Medium
c
\(\begin{array}{l}
\,\,\,\,\,\,\,\,Given,\,{P_i} = {P_f} = mV\\
chenge\,in\,momentum\,of\,the\,ball\\
= \,{{\bar P}_f} - {{\bar P}_i}\\
= \left( { - {P_{fx}}\hat i - {P_{fy}}\hat j} \right) - \left( {{P_{ix}}\hat i - {P_{iy}}\hat j} \right)\\
= - \hat i\left( {{P_{fx}} + {p_{ix}}} \right) - \hat j\left( {{p_{fy}} - {p_{iy}}} \right)\\
= - 2{P_{ix}}\hat i = - mV\hat i\,\,\,\left[ {{P_{fy}} - {P_{iy}} = 0} \right]
\end{array}\)
\(\begin{array}{l}
\,\,\,\,\,\,\,\,Given,\,{P_i} = {P_f} = mV\\
chenge\,in\,momentum\,of\,the\,ball\\
= \,{{\bar P}_f} - {{\bar P}_i}\\
= \left( { - {P_{fx}}\hat i - {P_{fy}}\hat j} \right) - \left( {{P_{ix}}\hat i - {P_{iy}}\hat j} \right)\\
= - \hat i\left( {{P_{fx}} + {p_{ix}}} \right) - \hat j\left( {{p_{fy}} - {p_{iy}}} \right)\\
= - 2{P_{ix}}\hat i = - mV\hat i\,\,\,\left[ {{P_{fy}} - {P_{iy}} = 0} \right]
\end{array}\)
\(\begin{array}{l}
Here,\,{P_{ix}} = {P_{fx}} = {P_i}\cos {60^ \circ } = \frac{{mV}}{2}\\
{\rm{Impulse}}\,{\rm{imparted}}\,{\rm{by}}\,{\rm{the}}\,{\rm{wall}}\,\\
= change\,in\,the\,momentum\,of\\
the\,ball\, = \,mV.
\end{array}\)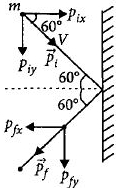
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$200 \,m / s$ ની ગતિથી ચાલતી $10 \,g$ દળની એક ગોળી લાકડાના પાટિયામાં $5 \,cm$ સુધી ઘૂસીને અટકી જાય છે. ગોળી પર લાગેલો સરેરાશ બળ ................ $N$ હશે.View Solution
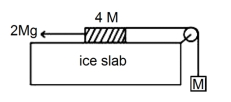
- 2દોરી-પુલી રચનાની મદદથી લટકાવેલ $M$ દળ ચાર ગણું વધારે દળ સાથે જોડાયેલ છે. આ મોટા દળને સમક્ષિતિજ બરફના ચીસલા ઉપર મૂકવામાં આવેલ છે અને તેને $2 \,Mg$ બળ વડે ખેંચવામાં આવે છે. આ પરિસ્થિતિમાં દોરીમાં તણાવ $\frac{x}{5} Mg$ મળે છે. $x$ નું મૂલ્ય ........... હશે. દોરીનું દળ અવગણો અને મોટા ચોસલા (મોટું દળ) અને બરફની પાટ વચ્ચે ધર્ષણ અવગણો. (Given $g=$ acceleration due to gravity)View Solution
- 3શિરોલંબની ઉડાન માટે $600\; kg$ નું રોકેટ તૈયાર કરેલ છે. જો બહાર નીકળતા વાયુની ઝડપ $1000\; m/s$ હોય, તો તેના વજનને ઊંચકાવવા માટે જરૂરી બળ પૂરું પાડવા પ્રતિ સેકન્ડે કેટલો વાયુ ($kg\,s^{-1}$ માં) બહાર કાઢવો જોઈએ?View Solution
- 4$60gm$ દળનો દડો દીવાલ સાથે $4m/s$ ના વેગથી અથડાઇને તે જ વેગથી પાછો આવે,તો વેગમાનમાં થતો ....$kg{\rm{ - }}m/s$ ફેરફારView Solution
- 5$10\,kg$ દળ ઘરાવતી વસ્તુને સમક્ષિતિજની સાપેક્ષે $45^{\circ}$ ના કોણે પ્રક્ષિપ્ત કરવામાં આવે છે. વસ્તુના ગતિપથને અવલોક્તા તે $(20,10)$ બિંદુમાંથી પસાર થાય છે. જો તેના ગતિપથનો સમય $T$ હોય,તો $t=\frac{T}{\sqrt{2}}$ સમયે વેગમાન સદિશ $............$ થશે.$\left[\right.$ $\left.g=10 m / s ^{2}\right]$ લો.View Solution
- 6રોકેટ $500 \,m/s$ ના વેગથી પ્રતિ સેકન્ડે $50 \,g$ વાયુ બહાર કાઢે છે.તો રોકેટ પર ......... $N$ બળ લાગતું હશે.View Solution
- 7$50 \,g$ દળનાં એેક દડાને $20\,m$ ની ઉંચાઈથી ફેકવામાં આવે છે. એક જમીન પર ઉભેલો છોકરો $200 \,N$ નાં સરેરાશ બળ સાથે બેટથી દડાને શિરોલંબ રીતે ઉપર તરફ મારે છે. જેથી તે $45 \,m$ ની શિરોલંબ ઉંચાઈને પ્રાપ્ત કરે છે. તો દડાનો બેટ સાથેનો સંપર્ક સાથે રહેવાનો સમય શોધો.View Solution
[ $g=10 \,m / s ^2$ લો]
- 8કોઈ $m$ દળના કણ પર પ્રયોગમુલક નિયમ પ્રમાણે બળ $F = \frac{R}{{{t^2}}}\,v(t)$ લગાવવામાં આવે છે. ગતિની શરુઆતની સ્થિર સ્થિતિ થી પ્રાયોગિક રીતે આ નિયમ ની કસોટી કરવી હોય તો તેના માટે ..... નો વક્ર દોરવો એ ઉત્તમ રસ્તો છે.View Solution
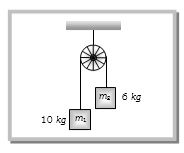
- 9આપેલ તંત્ર માટે તંત્રનો પ્રવેગ ........... $ms^{-2}$ થાય.View Solution
- 10$0.1\, kg$ દળ અને $10$ $m / s$નો વેગ ધરાવતી ગોળી લાકડાના બ્લોકમાં $50\, cm$ સુધી ઘુસીને સ્થિર થાય છે,તો તેના પર લાગતું અવરોધક બળ $'x' \,N$ છે ,તો $'x'............... \,N$View Solution
