નીચે આપેલા વિધાનોમાં, પ્રથમ ક્રમની પ્રક્રિયા માટેના અર્ધ-આયુષ્ય સમય વિશેનું યોગ્ય વિધાન કયું છે ?
AIIMS 2018, Medium
a
For a first order reaction, the integrated rate law is written as,
For a first order reaction, the integrated rate law is written as,
\(k=\frac{2.303}{t} \log \frac{a}{a-x}\)
Where, \(k=\) Rate constant
\(a=\) initial concentration
\(a-x=\) concentration after time \({ }^{\prime} t^{\prime}\)
For half-life, \(t=t_{1 / 2}, x=\frac{a}{2}\)
On substituting the values, we get
\(k=\frac{2.303}{t_{1 / 2}} \log \frac{a}{a-\frac{a}{2}}=\frac{2.303}{t_{1 / 2}} \log 2\)
\(=\frac{0.693}{t_{1 / 2}}\)
\(k=\frac{0.693}{t_{1 / 2}}\)
Thus, \(t_{1/2}\) of a first order reaction does not depend upon the concentration.
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
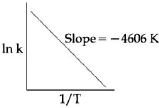
- 1એક પ્રક્રિયા માટે $ln k$ વિરૂદ્ધ $1/T$ નો આલેખ ધ્યાનમાં લો જ $400\, K$ એ આ પ્રક્રિયાનો વેગ અચળાંક $10^{-5}\,s^{-1},$ હોય, તો $500\, K$ એ વેગ અચળાંક કેટલો હશે?View Solution
- 2જો પ્રક્રિયક $'A'$ની સાંદ્રતા બમણી કરવાથી પ્રક્રિયા વેગ $4$ ગણો વધે છે અને $'A'$ ની સાંદ્રતા ત્રણ ગણી વધારતા $9$ ગણો વધે છે, તો દર કોના પ્રમાણમાં છે?View Solution
- 3જ્યારે તાપમાન $40^{\circ} C$ થી $30^{\circ} C$માં બદલાયું ત્યારે પ્રક્રિયા વેગમાં $3.555$ ગણો ઘટાડો થયો.ત્યારે પ્રક્રિયાની સક્રિયકરણ ઊર્જા ...............$kJ\, mol ^{-1}$ છેView Solution
[લો; $R =8.314 \,J\, mol ^{-1}\, K ^{-1}$ In $3.555=1.268$]
- 4$2O_3 \rightarrow 3O_2$ રાસાયણિક પ્રક્રિયા નીચે મુજબ દર્શાવી છે. તો દર નિયમ સમીકરણ..... થશે.View Solution
$ O_3 $ $\rightleftharpoons$ $ O_2 + O$ ...... (ઝડપી) ;
$O + O_3 \rightarrow 2O_2$ ...... (ધીમી)
- 5પ્રયોગશાળામાં એક જીવરાસાયણિક પ્રક્રિયા માનવશરીરની બહાર ઉત્સેચકની ગેરહાજરીમાં કરતાં તેનો વેગ, $10^{-6}$ ગણો મળે છે. જો આ પ્રક્રિયા ઉત્સેચકની હાજરીમાં કરવામાં આવે તો પ્રક્રિયાની સક્રિયકરણ ઉર્જા કેટલી થશે ?View Solution
- 6પ્ર્કિયકની શરૂઆતની સાંદ્રતા $0.02\, M$ ધરાવતા એક શૂન્ય ક્રમની પ્રક્રિયાનો અર્ધઆયુષ્ય સમય $100\, s$ છે. તો પ્રક્રિયા માટે વેગ અચળાંક ($mol\, L ^{-1} s ^{-1}$ માં$)$ જણાવો.View Solution
- 7View Solutionજો પ્રક્રિયકની મૂળ સાંદ્રતા બમણી કરવામાં આવે તો તેનો અર્ધ-આયુષ્ય સમય પણ બમણો થાય છે, તો પ્રક્રિયાક્રમ દર્શાવો.
- 8View Solutionરાસાયણિક પ્રક્રિયા માટે કયો અપૂર્ણાંક કદાપિ હોઈ શકે નહિ?
- 9પ્રથમ ક્રમની પ્રક્રિયાનો દર અચળાંક $4 \times 10^{-3}$ સેકન્ડ $^{-1}$ છે તો પ્રક્રિયકની સાંદ્રતા $0.02 \,M$ છે તો પ્રક્રિયાનો દર શું થશે?View Solution
- 10આપેલ પ્રક્રિયા માટે $'a'$ ની જુદીજુદી પ્રારંભિક સાંદ્રતા એ $t_{1/2}$ ની માહિતીનો ક્રમ જુદોજુદો હોય છે. જે $[t_{1/2}\,\alpha \,a] $ અચળ હશે તો પ્રક્રિયાનો ક્રમ ....... હશે.View Solution
