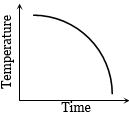
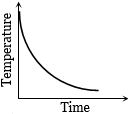
પદાર્થને ગરમ કરીને વાતાવરણમાં મૂકતાં તેનાં તાપમાન વિરુધ્ધ સમયનો આલેખ
Diffcult
b
(b) According to Newton's law of cooling Rate of cooling \(\propto\) Temperature difference
(b) According to Newton's law of cooling Rate of cooling \(\propto\) Temperature difference
==> \( - \frac{{d\theta }}{{dt}} \propto (\theta - {\theta _0})\)
==>\( - \frac{{d\theta }}{{dt}}\)=\(\alpha \;(\theta - {\theta _0})\) (\(\alpha\)= constant)
==> \(\int\limits_{{\theta _i}}^\theta {\frac{{d\theta }}{{(\theta - {\theta _0})}} = - \alpha \int\limits_0^t {dt} } \)
==> \(\theta = {\theta _0} + ({\theta _i} - {\theta _0}){e^{ - \alpha \,t}}\)
This relation tells us that, temperature of the body varies exponentially with time from \({\theta _i}\) to \({\theta _0}\) Hence graph \((b)\) is correct.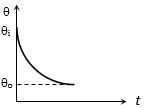
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionસંપૂર્ણ સૂર્યગ્રહણ દરમિયાન ફોનહોફર રેખાઓ સ્પષ્ટ દેખાય છે કારણ કે.....
- 2એક પાતળા ધાતુના કવચની ત્રીજ્યા $r$ અને તાપમાન $T$ જેટલું ગરમ કરવામાં આવે છે અને પછી ઠંડુ પાડવામાં આવે છે. કવચના ઠંડા પડવાનો દર કોના સમપ્રમાણમાં હશે?View Solution
- 3એક $25^{\circ} {C}$ તાપમાનવાળી મોટી રૂમમાં રહેલ પદાર્થનું તાપમાન $80^{\circ} \mathrm{C}$ થી $70^{\circ} \mathrm{C}$ થતાં $12$ મિનિટ લાગે છે. સમાન પદાર્થનું તાપમાન $70^{\circ} \mathrm{C}$ થી $60^{\circ} \mathrm{C}$ થતાં લગભગ કેટલો સમય ($min$ માં) લાગશે?View Solution
- 4સૂર્યમાંથી નીકળતી ઊર્જાએ પૃથ્વીની સપાટી પર $20\, \frac{{kcal}}{{{m^2}\;min}}$ ના દરે લંબ રૂપે આપાત થાય છે. જો સૂર્યનું તાપમાન અત્યાર કરતાં બમણું થાય, તો પૃથ્વીની સપાટી પર લંબરૂપે આપાત થતી ઉત્સર્જન ઊર્જા ($kcal/m ^2 \,min$ માં) કેટલી થાય?View Solution
- 5જો સપાટી પરના ટ્રાન્સમીશના પાવર $\frac{1}{9}$ હોય અને પ્રતિબીંબીત પાવર $\frac{1}{6}$ છે, તો શોષણ પાવર .........View Solution
- 6જુદા જુદા દ્રવ્યોના બનેલા બે ગોળાઓમાં પ્રથમ ગોળાની ત્રિજ્યા બીજા ગોળાની ત્રિજ્યા કરતાં બમણી અને દીવાલની જોડાઈ ચોથા ભાગની છે. તેમને સંપૂર્ણપણે બરફથી ભરી દેવામાં આવે છે. જો મોટી ત્રિજ્યા ધરાવતા ગોળાના બરફને સંપૂર્ણપણે પીંગળતાં લાગતો સમય $25 min$ અને નાની ત્રિજ્યા ધરાવતા ગોળાના બરફને સંપૂર્ણપણે પીંગળતાં લાગતો સમય $16 min$ હોય, તો મોટા અને નાના ગોળાનાં દ્રવ્યોની ઉષ્માવાહકતાનો ગુણોત્તર ..........View Solution
- 7જો તારાની ત્રીજ્યા $R$ હોય અને તે કાળા પદાર્થની જેમ વર્તતો હોય. તારાનું તાપમાન કેટલુ હોય જો $Q$ જેટલા દરથી ઉર્જા ઉત્પન્ન કરતી હોય તો ? ( $\sigma$ સ્ટીફન અચળાંક છે.)View Solution
- 8સ્થાયી ઉષ્મા અવસ્થામાં રહેલો ધાતુનો સળિયો તેના એક છેડેથી બીજા છેડે ઉષ્માનું વહન કરે છે. સળિયાના ગરમ છેડાથી $x$ લંબાઈ મુજબ તેના તાપમાન $\theta$ માં થતા ફેરફરરનો આલેખ નીચેનામાંથી કેવો હશે?View Solution
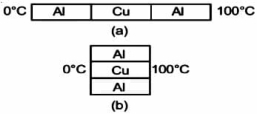
- 9ત્રણ સળીયા આકૃતિમાં દર્શાવ્યા મુજબ અલગ અલગ છે. જો આકૃતિ $(a)$ માં ગરમ બાજુનો ઉષ્મા દર $40 \,W$ જેટલો છે. આકૃતિ $(b)$ માં દર્શાવ્યા મુજબ એકબીજાના સંપર્કમાં હોય ત્યારે ઉષ્માપ્રવાહ ............. $W$. ધારો $K_{A l}=200 \,W / m { }^{\circ} C$ and $\left.K_{ cu }=400 \,W / m ^{\circ} C \right)$View Solution
- 10એક પાત્રમાં $100°\,C$ તાપમાને ગરમ પાણી ભરેલ છે. જો $T_1$ સમયમાં તેનું તાપમાન ઘટીને $80°\,C$ થાય છે અને $T_2$ સમયમાં તેનું તાપમાન ઘટીને $80°\,C$ થી $60°\,C$ થાય છે, તો ......View Solution