As \(\mu=\frac{\sin \left(\frac{A+\delta_{m}}{2}\right)}{\sin \left(\frac{A}{2}\right)}\)
\(\mu = \frac{{\sin \left( {\frac{{A + A}}{2}} \right)}}{{\sin \left( {\frac{A}{2}} \right)}}\) \( = \frac{{\sin A}}{{\sin \left( {\frac{A}{2}} \right)}}\) \(\left( {\because {\delta _m} = A({\text{ Given }})} \right)\)
\( = \frac{{2\sin \left( {\frac{A}{2}} \right)\cos \left( {\frac{A}{2}} \right)}}{{\sin \left( {\frac{A}{2}} \right)}}\) \( = 2\cos \left( {\frac{A}{2}} \right)\)
As \(\delta=i+e-A\)
At minimum deviation, \(\delta=\delta_{m}, i=e\)
\(\therefore {\delta _m} = 2i - A\)
\(2i = {\delta _m} + A\)
\(i = \frac{{{\delta _m} + A}}{2} = \frac{{A + A}}{2} = A\) \(\left( {\because \,\,{\delta _m} = A({\text{ given }})} \right)\)
\({i_{\min }} = {0^o} \Rightarrow {A_{\min }} = {0^o}\)
Then, \(\mu_{\max }=2 \cos 0^o=2\)
\(\therefore \) \(i_{\max }=\frac{\pi}{2} \Rightarrow A_{\max }=\frac{\pi}{2}\)
Then, \(\mu_{\min }=2 \cos 45^o=2 \times \frac{1}{\sqrt{2}}=\sqrt{2}\)
Download our appand get started for free
Similar Questions
- 1$f$ કેન્દ્રલંબાઇ ધરાવતા બર્હિગોળ લેન્સને આકૃતિ મુજબ કાપતાં એક ટુકડાની કેન્દ્રલંબાઇ કેટલી થાય?View Solution

- 2$12cm$ ઊંડાઇ પર રહેલ માછલીને જોતાં માછલીનું પ્રતિબિંબ કેટલા ......$cm$ ઊંચાઇ પર દેખાશે?View Solution
- 3પાત્રમાં પ્રવાહી $120\,mm$ ઊંચાઇ સુધી ભરેલ છે.તેમાં રહેલ સોય $80\,mm$ ઊંડાઇ પર દેખાતી હોય,તો પ્રવાહીનો વક્રીભવનાંક કેટલો હશે?View Solution
- 4'$d$' ઊંડાઈના પાત્રમાં અડધે સુધી $n _1$ વક્રીભવનાંક ધરાવતું તેલ, અને બાકીનો અડધો ભાગ $n _2$ વક્રીભવનાંક ધરાવતા પાણીથી ભરવામાં આવે છે.જ્યારે આા પાત્રમાં ઉપરથી જોતાં તેની દેખાતી ઊંડાઈ $.........$ થશે.View Solution
- 5બર્હિગોળ લેન્સ દ્વારા વસ્તુનું પ્રતિબિંબ ${I_1}$ ઊંચાઇનું મળે છે.હવે લેન્સને બીજા સ્થાને મૂકતાં વસ્તુનું પ્રતિબિંબ ${I_2}$ ઊંચાઇનું મળે છે,તો વસ્તુની ઊંચાઇ કેટલી હશે?View Solution
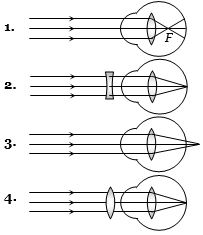
- 6View Solutionઉપરનામાંથી કઇ આકૃતિ ખોટી માહિતી આપે છે?
- 7એક પડદાથી નિયત(fix) અંતરે વસ્તુ પડેલ છે એક પાતળા લેન્સ ના બે સ્થાન ($10\, cm$ અંતરે) માટે વસ્તુનું પડદા પર પ્રતિબિંબ મળે છે. આ લેન્સના બે સ્થાન માટે મળતા પ્રતિબિંબ $3 : 2$ના પરિમાણમાં મળે છે. તો વસ્તુ અને પડદા વચ્ચેનું અંતર કેટલા $cm$ હશે?View Solution
- 8એક સમતલ બહિર્ગોળ લેન્સનો વક્રીભવનાંક $1.6$ છે.આ લેન્સની વક્રસપાટીની વક્રતાત્રિજયા $60\,cm$ છે. લેન્સની કેન્દ્રલંબાઇ ($cm$ માં) કેટલી હશે?View Solution
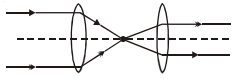
- 9આકૃતિમાં અમુક અંતરે રહેલા બે લેન્સ માટે કિરણાકૃતિ આપેલ છે. નિચેનામાંથી ક્યો વિકલ્પ સાચો છે ? ( $f_1, f_2=$ કેન્દ્રલંબાઈ, $d=$ લેન્સ વચ્ચેનું અંતર)View Solution
- 10સમાન કેન્દ્રલંબાઈ $(f)$ના પાતળા લેન્સ,પણ એક બહિર્ગોળ અને બીજો અંતર્ગોળ એક્બીજાના સંપર્કમાં રાખેલ છે. આ સંયોજનની સમતુલ્ય કેન્દ્રલંબાઈ $.......$ થાય.View Solution
