| Run | $[A]/mol\,L^{-1}$ | $[B]/mol\,L^{-1}$ | $D$ ઉત્પન્ન થવાનો શરૂઆતનો દર $mol\,L^{-1}\,min^{-1}$ |
| $I.$ | $0.1$ | $0.1$ | $6.0 \times 10^{-3}$ |
| $II.$ | $0.3$ | $0.2$ | $7.2 \times 10^{-2}$ |
| $III.$ | $0.3$ | $0.4$ | $2.88 \times 10^{-1}$ |
| $IV.$ | $0.4$ | $0.1$ | $2.40 \times 10^{-2}$ |
ઉપરની વિગત પરથી નીચેનામાંથી ક્યું સાચુ છે ?
Let the order of reaction with respect to $\mathrm{A}$ is $\mathrm{x}$
and with respect to $\mathrm{B}$ is $y$.
Thus,
rate $=\mathrm{k}[A]^{x}[B]^{y}$
($x$ and $y$ are stoichiometric coefficient)
For the given cases,
$I$. rate $=\mathrm{k}(0.1)^{x}(0.1)^{y}=6.0 \times 10^{-3}$
$II$. rate $=\mathrm{k}(0.3)^{x}(0.2)^{y}=7.2 \times 10^{-2}$
$III$. rate $=\mathrm{k}(0.3)^{x}(0.40)^{y}=2.88 \times 10^{-1}$
$IV$. rate $=\mathrm{k}(0.34)^{x}(0.1)^{y}=2.40 \times 10^{-2}$
Dividing Eq. $(I)$ by Eq. $(IV)$, we get
$\left(\frac{0.1}{0.4}\right)^{x}\left(\frac{0.1}{0.1}\right)^{y}$
$\frac{6.0 \times 10^{-3}}{2.4 \times 10^{-2}}$
$\left(\frac{1}{4}\right)^{x} =\left(\frac{1}{4}\right)^{1}$
$\therefore x=1$
On dividing Eq. $(II)$ by Eq. $(III)$, we get
$\left(\frac{0.3}{0.3}\right)^{x}\left(\frac{0.2}{0.4}\right)^{y}=\frac{7.2 \times 10^{-2}}{2.88 \times 10^{-1}}$
$\left(\frac{1}{2}\right)^{y}=\frac{1}{4}$
$\left(\frac{1}{2}\right)^{y}=\left(\frac{1}{2}\right)^{2}$
$\therefore y=2$
Thus, rate law is,
$\text {rate} =k[A]^{1}[B]^{2}$
$=k[A][B]^{2}$
Download our appand get started for free
Similar Questions
- 1પ્રક્રિયા, $a A +b B \rightarrow c C +d D$ માટે, આલેખ $\log \,k$ વિરૂધ્ધ $\frac{1}{ T }$ ને નીચે આપેલ છેView Solution
કયા તાપમાને $(K$ માં) પ્રક્રિયાનો વેગ અચળાંક $10^{-4} s ^{-1}$ થશે તે શોધો ?(નજીકના પૂર્ણાંકમાં રાઉન્ડ ઑફ)
[આપેલ : $500\, K$ પર, પ્રક્રિયાનો વેગ અચળાંક $10^{-5} s^{-1}$ છે.]
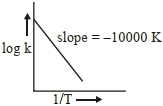
- 2પ્રક્રિયા ${H_2}(g) + {I_2}(g)$ $\rightleftharpoons$ $2HI(g)$, માટે વિકલનીય વેગનિયમ.. . થસે.View Solution
- 3$C_2H_5I + OH \rightarrow C_2H_5OH + I^{-}$ પ્રક્રિયા માટે $30^o$ સે. અને $60^o$ સે. તાપમાને વેગ અચળાંકના મલ્યો અનુક્રમે $0.325$ અને $6.735$ લિટર મોલ$^{-1}$ સેકન્ડ $^{-1} $ હોય તો સક્રિયકરણ ઊર્જા $(E_a)$ નું મૂલ્ય .......... કેલરી થશે.View Solution
- 4પ્રથમ ક્રમની પ્રક્રિયા માટે અર્ધઆયુષ્ય સમય $6$ મિનિટ છે. તો પ્રક્રિયાનો દર અચળાંક શોધો.View Solution
- 5સામાન્ય રીતે, પાછળની અને આગળની પ્રતિક્રિયાઓ માટે, સક્રિયકરણ શક્તિઓ ${E_b}$ અને ${E_f}$ સાથે, ઉષ્માશોષક પ્રક્રિયા $X$ થી $Y$ ધ્યાનમાં લોView Solution
- 6$273\, K$ તાપમાને એક પ્રક્યિાનો વેગ $R_0$, છે. તો $313\, K$ તાપમાને પ્રક્રિયાનો વેગ કેટલો થશે ? (તાપમાન ગુણક $2$ લેવો)View Solution
- 7View Solutionજો પ્રક્રિયાનો વેગ એ વેગ અચળાંક બરાબર હોય તો પ્રક્રિયાનો ક્રમ .... થશે.
- 8પ્રકિયા માટેView Solution
$2{N_2}{O_5}\, \to \,4N{O_2}\, + \,{O_2}$
પ્રકિયા નો દર શું હશે ?
- 9એક રાસાયણિક પ્રક્રિયાનો વેગ અચળાંક, પ્રક્રિયાના તાપમાનમાં $9\, K$નો વધારો કરતા બમણો માલૂમ પડયો.જો પ્રક્રિયા $300\, K$ તાપમાને થતી હોય તેમ ધારીએ તો, સક્રિયકરણ ઊર્જાનુ મૂલ્ય............$k\,J\, mol ^{-1}$ થાય. [નજીકનો પૂર્ણાંક]View Solution
(આપેલું છે$: \ln 10=2.3, R =8.3 \,J\, K ^{-1} \,mol ^{-1}, \log 2=0.30$ )
- 10જો પ્રક્રિયાનો $t_{1/2} = 69.3$ સેકન્ડ છે અને દર અચળાંક $10^{-2}$ પ્રતિ સેકન્ડ છે તો પ્રક્રિયા ક્રમ.......View Solution
