પ્રક્રિયા :
$2N_2O_5 \rightarrow 4NO_2 + O_2$ નો દર ત્રણ રીતે લખી શકાય.
$\frac{-d[N_2O_5 ]}{dt} = k[N_2O_5]$
$\frac{d[NO_2 ]}{dt} = k'[N_2O_5]\,;$ $\frac{d[O_2 ]}{dt} = k"[N_2O_5]$
$k$ અને $k'$ તથા $k$ અને $k''$ વચ્ચેનો સંબંધ .............
AIPMT 2011, Diffcult
Download our app for free and get started
b
Rate of disappearance of reactants \(=\) Rate of appearance of products
Rate of disappearance of reactants \(=\) Rate of appearance of products
\(=\frac{1}{2} \frac{d\left(N_{2} O_{5}\right)}{d t}=\frac{1}{4} \frac{d\left(N O_{2}\right)}{d t}=\frac{d\left(O_{2}\right)}{d t}\)
\(=\frac{1}{2} k\left(N_{2} O_{5}\right)=\frac{1}{4} k'\left(N_{2} O_{5}\right)=k''\left(N_{2} O_{5}\right)\)
\(\Rightarrow \frac{k}{2}=\frac{k'}{4}=k''\)
\(\Rightarrow k'=2 k\), \(k''=\frac{k}{2}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
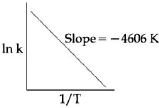
- 1એક પ્રક્રિયા માટે $ln k$ વિરૂદ્ધ $1/T$ નો આલેખ ધ્યાનમાં લો જ $400\, K$ એ આ પ્રક્રિયાનો વેગ અચળાંક $10^{-5}\,s^{-1},$ હોય, તો $500\, K$ એ વેગ અચળાંક કેટલો હશે?View Solution
- 2પ્રથમ ઓર્ડર પ્રક્રિયા માટે $A \rightarrow 2 B$માં $100$ મિનિટ પછી $1$ મોલ પ્રક્રિયક $A$ પછી $B$ ના $0.2$ મોલ્સ આપે છે. પ્રક્રિયાનું અર્ધઆયુષ્ય $.....\,min$ છે. [ઉપયોગ કરો $: \ln 2=0.69, \ln 10=2.3$View Solution
$log$નો ગુણધર્મ $\ln \left(\frac{{x}}{{y}}\right)=\ln {x}-\ln {y}$
- 3View Solutionબે જુદાંજુદાં પ્રક્રિયકો વચ્ચેની પ્રક્રિયા ..... હોતી નથી.
- 4View Solutionજો પ્રથમ અને શૂન્ય કમની પ્રકિયાના અર્ધઆયુષ્ય સમય સમાન હોય, તો પ્રક્રિયાની શરૂઆતમાં પ્રકિયા વેગનો ગણોતર ............. થશે.
- 5$A\left( g \right) \rightleftharpoons B\left( g \right)$ સંતુલન માટે $\Delta H$ , $-40\, k\,J/mol$ છે. જો પૂરોગામી અને પ્રતિમાની પ્રક્રિયાની સક્રિયકરણ ઊર્જા $(E_f)$ અને $(E_b)$ નો ગુણોત્તર $\frac{2}{3}$ હોય, તો ...View Solution
- 6View Solutionત્રણ પગલાની પ્રક્રિયા માટે ઉર્જાના આલેખની આકૃતિ દોરો જેમાં પ્રથમ પગલું સૌથી ધીમું અને છેલ્લું પગલું સૌથી ઝડપી છે. (ધારો કે પ્રકિયા ઉષ્માશોષક છે )
- 7પ્રક્રિયા $2N_2O_5\rightarrow 4NO_2 + O_2$ માટે નો દર અચળાંક $3.0 × 10^{-5 }s^{-1}$ છે. જો દર $2.40 × 10^{-5}$ મોલ $L^{-1} s^{-1}$ હોય,તો $N_2O_5$ ની સાંદ્રતા (મોલ $L^{-1}$) શોધો.View Solution
- 8$A$ અને $B$ પ્રથમ ક્રમ ગતિકી વડે વિઘટન પામે છે જેનો અર્ધ-આયુષ્ય અનુક્રમે $54.0\, min$ અને $18.0\, min$ છે. $A$ અને $B$ નાં અ-સક્રિય મિશ્રણમાં (જે માં પ્રક્રિયા ના થતી હોય તેવું મિશ્રણ) સમ મોલર થી શરૂઆત કરીએ તો, $A$ ની સાંદ્રતાં $B$ નાં કરતાં $16$ ગણી વધારે રહે તે માટેનો લાગતો સમય $..... \, min.$ છે. (નજીકનાં પૂર્ણાંકમાં રાઉન્ડ ઓફ કરો)View Solution
- 9$25 ^{\circ}\,C$ પર એક વાયુ $AB _3$ ના વિધટનનો અભ્યાસ એક વિદ્યાર્થીએ કર્યો તેને નીચે મુજબની માહિતી મેળવી.View Solution
$p ( mm Hg )$ $50$ $100$ $200$ $400$ સાપેક્ષ $t _{1 / 2}( s )$ $4$ $2$ $1$ $0.5$ પ્રક્રિયાનો ક્રમ શોધો.
- 10શૂન્ય ક્રમતી એક પ્રક્રિયાતો વેગ અચળાંક $2.0\times10^{-2}\, mol\, L^{-1}\, s^{-1}$ છે. જો $25\, seconds$ પછી પ્રક્રિયાની સાંદ્રતા $0.5\, M$ હોય તો શરૂઆતની સાંદ્રતા ......... $M$ માં શું હશે ?View Solution