પ્રક્રિયા, $a A +b B \rightarrow c C +d D$ માટે, આલેખ $\log \,k$ વિરૂધ્ધ $\frac{1}{ T }$ ને નીચે આપેલ છે
કયા તાપમાને $(K$ માં) પ્રક્રિયાનો વેગ અચળાંક $10^{-4} s ^{-1}$ થશે તે શોધો ?(નજીકના પૂર્ણાંકમાં રાઉન્ડ ઑફ)
[આપેલ : $500\, K$ પર, પ્રક્રિયાનો વેગ અચળાંક $10^{-5} s^{-1}$ છે.]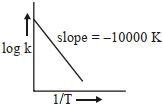
JEE MAIN 2021, Medium
Download our app for free and get started
b
$\log K =\log A -\frac{ Ea }{2.303 RT }$
$\log K =\log A -\frac{ Ea }{2.303 RT }$
$\mid$Slope$\mid=\frac{E a}{2.303 R }=10,000$
$\log \left(\frac{ K _{2}}{ K _{1}}\right)=\frac{ Ea }{2.303 R }\left(\frac{1}{ T _{1}}-\frac{1}{ T _{2}}\right)$
$\log \left(\frac{10^{-4}}{10^{-5}}\right)=10,000\left[\frac{1}{500}-\frac{1}{ T _{2}}\right]$
$T _{2}=526.31 \simeq 526 K$
Hence answer is $(526)$
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1બે પ્રક્રિયાઓ માટે પૂર્વઘાતાંક અવયવના મૂલ્યો સમાન છે.પરંતુ તેમની સક્રિયકરણ ઊર્જાતા મૂલ્યો વચ્ચે $24.9\, kJ\,mol^{-1}$ તો $300\, K$ તાપમાને તેમના વેગ અચળાંકોનો ગુણોત્તર ....View Solution
- 2જો $c_o$ પ્રક્રિયકની મૂળ સાંદ્રતા હોય, તો શૂન્ય ક્રમની પ્રક્રિયા માટે અર્ધઆયુષ્ય સમય શુ થશે ?View Solution
- 3$2 NO_{(g)} + Cl_{2(g)} \rightarrow 2NOCl_{(g)}$, પ્રક્રિયા માટે જ્યારે $Cl_2$ ની સાંદ્રતા બમણી થાય. પ્રક્રિયાનો દર વાસ્તવિક કરતા બે ગણો થાય છે. જ્યારે $NO$ ની સાંદ્રતા બમણી થાય ત્યારે દર ચાર ગણો થાય તો પ્રક્રિયાનો ક્રમ શું થશે?View Solution
- 4જો પ્રથમ ક્રમની પ્રક્રિયા માટે પ્રક્રિયકની સાંદ્રતા $ 'x'$ વધે છે તો $K = $………View Solution
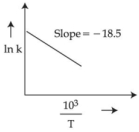
- 5$700 -$ $1000\,K$ તાપમાન શ્રેણીમાં (વિસ્તાર માં) એસિટાલ્ડીહાઈડના વિઘટન માટેના દર (વેગ) અચળાંક માપવામાં આવ્યાં. $\ln k$ વિરુદ્ધ $\frac{10^{3}}{ T }$ આલેખ દોરીને માહિતીનું પૃથ્થકરણ કરવામાં આવ્યું.પ્રક્રિયા માટે સક્રિયકરણ શક્તિનું મૂલ્ય $\dots\dots\dots$$kJ\,mol { }^{-1}$ છે.(નજીકનો પૂર્ણાંક)View Solution
(આપેલ:$R =8.31\,JK ^{-1}\,mol ^{-1}$)
- 6એક પ્રક્રિયાની સક્રિયકરણ શક્તિ જે $80.9 \,kJ \,mol^{-1}$ છે. તેમાં અણુઓનો એક અંશ (ભાગ) જે $700\, K$ પર, પ્રક્રિયા કરીને નીપજ બનવા માટે પૂરતા પ્રમાણમાં ઊર્જા ધરાવે છે તે $e ^{-x}$ છે. તો $x$નું મૂલ્ય ..... છે.View Solution
(નજીકના પૂર્ણાંકમાં રાઉન્ડ ઑફ) $[$ ઉપયોગ કરો : $\left. R =8.31 \,J \,K ^{-1} \,mol ^{-1}\right]$
- 7$H_2O_2$ ના વિઘટનની પ્રક્રિયાનો વેગ અચળાંક $3.66 \times 10^{-3}\,s^{-1}$ છે. જો $H_2O_2$ ની શરૂઆતની સાંદ્રતા $0.882\, M$ હોય, તો ........ $\sec$ એ તેની સાંદ્રતા $0.600\,M$ થશે.View Solution
- 8View Solutionનીચે આપેલા વિધાનોમાં, પ્રથમ ક્રમની પ્રક્રિયા માટેના અર્ધ-આયુષ્ય સમય વિશેનું યોગ્ય વિધાન કયું છે ?
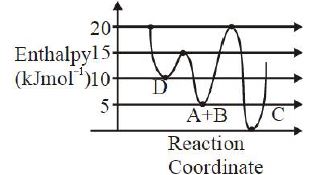
- 9$A$ અને $B$ વચ્ચેની નીચેની પ્રક્રિયાની એન્થાલ્પીનો આપેલ આલેખ ધ્યાનમાં લો. $A + B \to C + D$View Solution
ખોટું વિધાન ઓળખો.
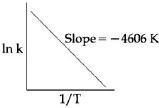
- 10એક પ્રક્રિયા માટે $ln k$ વિરૂદ્ધ $1/T$ નો આલેખ ધ્યાનમાં લો જ $400\, K$ એ આ પ્રક્રિયાનો વેગ અચળાંક $10^{-5}\,s^{-1},$ હોય, તો $500\, K$ એ વેગ અચળાંક કેટલો હશે?View Solution
