પ્રથમ ક્રમ ની પ્રકિયા નો અચળ વેગ $\mathrm{k}$ છે સમય $(t)$ $99 \%$ પ્રકિયા પૂર્ણ કરવા માટે લાગતો સમય છે તો પ્રકિયા કઈ હશે ?
NEET 2019, Medium
Download our app for free and get started
c
For first order reaction
For first order reaction
$\mathrm{k}=\frac{1}{\mathrm{t}} \ln \left[\frac{\mathrm{A}_{\mathrm{o}}}{\mathrm{A}_{\mathrm{t}}}\right] \quad \begin{array}{ll}{\text { For } 99 \% \text { completion, }} \\ {[\mathrm{A}]_{\mathrm{o}}=100, \quad \mathrm{[A]}_{\mathrm{t}}=1}\end{array}$
$\mathrm{k}=\frac{1}{\mathrm{t}} \ln \left[\frac{100}{1}\right]$
$\mathrm{k}=\frac{2.303 \mathrm{log}_{10} 100}{\mathrm{t}}$
$\mathrm{k}=\frac{2.303 \times 2}{\mathrm{t}}$
$\mathrm{k}=\frac{4.606}{\mathrm{t}}$
$t=\frac{4.606}{k}$
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1પદાર્થ $A $ અને $B$ વચ્ચેનો પ્રક્રિયા દર સમીકરણ દર $= k[A]^n[B]^m$ આપેલ છે. જો $A$ ની સાંદ્રતા બમણી અને $B$ ની સાંદ્રતા શરૂઆતની સાંદ્રતાથી અડધી થાય તો પહેલાનાં દર કરતાં હાલનો દર ગુણોત્તર ... થાય.View Solution
- 2$A + B$ $\rightleftharpoons$ $AB$ જો પ્રક્રિયાના $A$ અને $B$ ની સાંદ્રતા બમણી હોય તો પ્રક્રિયાનો દર ....... થશે.View Solution
- 3$A + 2B $ $\rightleftharpoons$ $ 2C + D$ પ્રક્રિયામાં $A$ ની સાંદ્રતા ચાર ગણી વધે અને $B$ ની સાંદ્રતા ઘટીને અડધી થાય તો પ્રક્રિયાનો દર = ........View Solution
- 4એસિડ દ્રાવણમાં થતા એસિટોનના બ્રોમીનેશનને નીચેના સમીકરણ વડે દર્શાવાય છે.View Solution
$CH_3COCH_{3(aq)} + Br_{2(aq)} \rightarrow $$CH_3COCH_2Br_{(aq)} + H^+_{(aq)}+ Br^-_{(aq)}$
નીચેની પ્રક્રિયા સાંદ્રતા પરથી આ ગતિકીય માહિતી મળે છે.
શરૂઆતની સાંદ્રતા, $M$
$[CH_3COCH_3]$ $[Br_2]$ $[H^+]$ $0.30$ $0.05$ $0.05$ $0.30$ $0.10$ $0.05$ $0.30$ $0.10$ $0.10$ $0.40$ $0.05$ $0.20$ $Br_2$ ના દૂર થવાનો શરૂઆતનો દર $Ms^{-1}$ માં નીચે મુજબ છે.
$5.7 \times 10^{-5} ,$ $5.7 \times 10^{-5} ,$ $1.2 \times 10^{-5} ,$ $3.1 \times 10^{-5}$
આ માહિતીને આધારે વેગ સમીકરણ ...... થશે.
- 5View Solutionઅથડામણના સિધ્ધાંત મુજબની નીચેના પૈકી કયું વિધાન સાચું નથી. ?
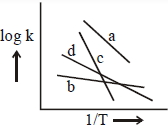
- 6ચાર જુદી જુદી પ્રક્રિયાઓ માટે વેગ અચળાંક વિરુદ્ધ $\frac{1}{\mathrm{T}}$ ના નીચેના આલેખ ધ્યાનમાં લો. તો આ પ્રક્રિયાઓની સક્રિયકરણ ઊર્જાઓ માટે નીચેના પૈકી ક્યો ક્રમ સાચો છે ?View Solution
- 7મનુષ્યનાં શરીરમાં $24$ કલાક પછી રેડીયોએક્ટિવ પદાર્થની $0.01 \mu $ ક્રિયાશીલતા જરૂરી છે. તે રેડીયોએક્ટિવનો અર્ધઆયુ $6 $ કલાક છે. તો રેડીયોએક્ટિવ પદાર્થનો મહત્તમ ક્રિયાશીલતા કેટલી દાખલ કરી શકાય?View Solution
- 8પ્રક્રિયા $XA + YB \rightarrow mp + nq$ માટે વેગ $= K[A]^c[B]^d$ તો કુલ પ્રક્રિયા ક્રમ કયો હશે ?View Solution
- 9પ્રક્રિયા${H_{2\left( g \right)}} + {I_{2\left( g \right)}} \to 2H{I_{\left( g \right)}}$ માટેની શક્ય ક્રિયાવિધિ નીચે મુજબ છે.View Solution
${I_2}\,\underset{{{K_{ - 1}}}}{\overset{{{K_1}}}{\longleftrightarrow}}\,2I\,$ (fast step)
$2I + {H_2}\xrightarrow{{{K_2}}}2HI$ (slow step)
તો પ્રક્રિયાનો વેગનિયમ જણાવો.
- 10જો તાપમાન $300\, K$ થી $310\, K$ કરવામાં આવે તો રાસાયણિક પ્રક્રિયાનો વેગ બમણો થાય છે. આ પ્રક્રિયાની સક્રિયકરણ શક્તિ .......... $kJ\, mol^{-1}$ થશે .View Solution
$(R= 8.314\,JK^{-1} \,mol^{-1}$ and $\log 2=0.301)$