પૃથ્વીની સપાટીથી કેટલી ઊંચાઈએ પદાર્થનું વજન સપાટીથી તેટલી જ ઊંડાઈ પરના વજન બરાબર થાય. જ્યાં $R$ પૃથ્વીની ત્રિજ્યા છે?
JEE MAIN 2024, Diffcult
Download our app for free and get started
d
\( g_p=\frac{g R^2}{(R+h)^2} \)
\( g_p=\frac{g R^2}{(R+h)^2} \)
\( g_q=g\left(1-\frac{h}{R}\right) \)
\( g_p=g_q \)
\( \frac{g}{\left(1+\frac{h}{R}\right)^2}=g\left(1-\frac{h}{R}\right) \)
\( \left(1-\frac{h^2}{R^2}\right)\left(1+\frac{h}{R}\right)=1\)
Take \(\frac{\mathrm{h}}{\mathrm{R}}=\mathrm{x}\)
So
\( \mathrm{x}^3-\mathrm{x}+\mathrm{x}^2=0 \)
\( \mathrm{x}=\frac{\sqrt{5}-1}{2} \)
\( \mathrm{~h}=\frac{\mathrm{R}}{2}(\sqrt{5}-1)\)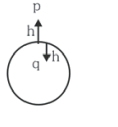
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1પૃથ્વીના કેન્દ્ર થી $8000 \,km$ ઊંચાઇ પર ગુરુત્વતીવ્રતા $6\,N/kg$ હોય તો ત્યાં ગુરુત્વસ્થિતિમાન કેટલું થાય?View Solution
- 2ગુરુત્વાકર્ષી ક્ષેત્રમાં, ગુરુત્વાકર્ષણ સ્થિતિમાન $V =-\frac{ K }{ x } \;( J / kg )$ દ્વારા આપવામાં આવે છે. બિંદુ $(2,0,3)\,m$ પર ગુરુત્વાકર્ષી ક્ષેત્રની તીવ્રતા કેટલી મળે?View Solution
- 3સૂર્યની આજુબાજુ ભ્રમણ કરતાં ગ્રહની કોણીય ઝડપ ($\omega$) અને અંતર $(r)$ હોય,તો ગ્રહનો ક્ષેત્રીય વેગ...View Solution
- 4પૃથ્વીની સપાટીથી ઉપર કોઈ બિંદુ આગળ ગુર્ત્વીય સ્થિતિમાન $-5.12 \times 10^7 \mathrm{~J} / \mathrm{kg}$ છે અને આ બિંદુ આગળ ગુરૂત્વાકર્ષણ પ્રવેગ $6.4 \mathrm{~m} / \mathrm{s}^2$ છે. પૃથ્વીનછી સરેરાશ ત્રિજ્યાં $6400 \mathrm{~km}$ છે તેમ ધારો. પૃથ્વીની સપાટીથી ઉપર આ બિંદૂની ઉંચાઈ__________થશે.View Solution
- 5જો પૃથ્વીની ત્રિજ્યા $6000\, km$ હોય તો સપાટી થી $6000 \,km $ ઊંચાઈએ પદાર્થનું વજન તેના સપાટી પરના વજન કરતાં...View Solution
- 6એક ગ્રહને સૂર્યને ફરતે એક પરિકમણ કરવા માટે $200$ દિવસ લાગે છે. જો ગ્રહનું સૂર્ય થી અંતર તેના મૂળ અંતર કરતા ચોથાભાગનું થાય ત્યારે એક પરિક્રમણ કરતા કેટલા દિવસો લાગશે ?View Solution
- 7View Solutionપૃથ્વી અને પૃથ્વી કરતાં બમણી ત્રિજ્યા અને ચૌથા ભાગની ઘનતા ધરાવતા ગ્રહ પર પદાર્થ ની નિષ્ક્રમણ ઝડપનો ગુણોત્તર કેટલો થાય?
- 8કોઈ એક ગ્રહ પર ગુરુત્વપ્રવેગના મૂલ્યમાં $4\%$ જેટલી ચોકચાઈ છે. $m$ દળ અને $T$ દોલનનો આવર્તકાળ ધરાવતા સાદા લોલકની ઉર્જાની ગણતરી કરવામાં આવે છે. જો તેના આવર્તકાળમાં $3 \%$ જેટલી ચોકચાઈ હોય તો, તેની ઉર્જા ${E}$ માં ચોકચાઈ કેટલા $\%$ હશે?View Solution
- 9એક ઉપગ્રહ પૃથ્વીની નજીકની વર્તુળાકાર કક્ષામાં ભ્રમણ કરે છે. જેની ત્રિજ્યા લગભગ પૃથ્વીની ત્રિજ્યા $R _{ e }$ જેટલી છે. ઉપગ્રહમાં રહેલ રોકેટને ફાયર કરતાં તેની ઝડપ તેની ગતિની દિશામાં અચાનક વધે છે જેના કારણે તે પહેલા કરતાં $\sqrt{\frac{3}{2}}$ ગણી થાય છે. જેથી તે પૃથ્વીના કેન્દ્રથી મહત્તમ $R$ અંતર સુધી પહોંચે છે તો $R$ નું મૂલ્ય $......R_e$ હશે?View Solution
- 10એક પદાર્થને $3R$ જેટલી ઊંચાઈ પરનાં બિંદુએથી સમક્ષિતિજ રીતે $\frac{1}{2} \sqrt{\frac{G M}{R}}$, ઝડપ સાથે પ્રક્ષિપ્ત કરવામાં આવે છે તો....View Solution