$R$ જેટલી મોટી ત્રિજ્યા ધરાવતા વર્તુળાકાર ગૂચળાના કેન્દ્ર આગળ એક ખૂબ નાની ત્રિજ્યા $r$ ધરાવતું ગુચળું મૂકેલું છે. બંને ગુચળા સમકેન્દ્રિય અને એક જ સમતલમાં છે. મોટા ગુચળામાંથી $I$ જેટલો પ્રવાહ વહે છે. નાનું ગુચળાને તેના સામાન્ય(common) વ્યાસની અક્ષને અનુલક્ષીને અચળ કોણીય વેગ $\omega $ થી ભ્રમણ કરવવામાં આવે છે. તો ભ્રમણના $t$ સમય પછી નાના ગુચળામાં કેટલું $emf$ પ્રેરિત થશે?
JEE MAIN 2018, Diffcult
c
According to Faraday's law of electromagnetic induction,
According to Faraday's law of electromagnetic induction,
\(e=-\frac{d \phi}{d t} \text { and } \phi=B A \cos \omega t=B \pi r^{2} \cos \omega t\)
\(\Rightarrow \quad e=-\frac{d}{d t}\left(\pi r^{2} B \cos \omega t\right)=\pi r^{2} B \sin \omega t(\omega)\)
\(\therefore e=\frac{\mu_{0} I}{2 R} \pi \omega r^{2} \sin \omega t\left(\because B=\frac{\mu_{0} I}{2 R}\right)\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
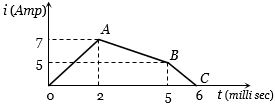
- 1$4.6\, H$ ઇન્ડકટરમાંથી પસાર થતા પ્રવાહનો આલેખ આપેલ છે,તો $t = 5 \,lmilli-sec$ થી $6 \,milli-sec$માં કેટલો $emf$ ઉત્પન્ન થાય?View Solution
- 2$50\,mH$ આત્મપ્રેરકત્વ ધરાવતી કોઇલમાં $2 \,A$ પ્રવાહ પસાર થતો હોય,તો તેમાં કેટલી ઊર્જાનો સંગ્રહ થાય?View Solution
- 3$C$ કેપેસીટી વાળા કન્ડેન્સરને $V_1$ વિદ્યુત સ્થીતીમાન સુધી ચાર્જ કરેલ છે હવે કન્ડેન્સરની પ્લેટને $L$ ઇન્ડકટન્સ ધરાવતા આદર્શ ઇન્ડકટર સાથે જોડવામાં આવેલ છે જ્યારે કન્ડેન્સરનો વિદ્યુત સ્થીતીમાન ઘટીને $V_2$ થાય તો ઇન્ડકટરમાંથી વહેતો પ્રવાહ શોધો ?View Solution
- 4$\oint {\vec B} .d\vec A\, = \,0$ નું કારણ કયું હશે ?View Solution
- 5$50\,H$ આત્મપ્રેરકત્વ ધરાવતી કોઇલને $10\,Ω$ અવરોધ સાથે જોડીને $2\,V$ની બેટરી સાથે લગાવવામાં આવે છે.ઘણા સમય પછી બેટરી દૂર કરતાં, પ્રવાહ $1/e$ માં ભાગનો થતાં કેટલા ......$seconds$ નો સમય લાગે?View Solution
- 6ટ્રાન્સફોર્મરના પ્રાથમિક ગૂંચળામાં આંટાની સંખ્યા $140$ અને ગૌણ આંટાની સંખ્યા $280$ છે,પ્રાથમિક ગૂંચળામાં પ્રવાહ $4\, A$ હોય તો ગૌણ ગૂચળામાં વહેતો પ્રવાહ ($A$ માં) કેટલો હશે?View Solution
- 7$L_{1}$ અને $L_{2}$ પ્રેરણ ધરાવતા બે ગૂંચળાને શ્રેણીમાં જોડવામાં આવ્યા છે, તેથી ગૂંચળાઆનું અન્યોન્ય પ્રેરણ $M$ છે. જો ગૂંચળામાં વિરુદ્ધ દિશામાં પ્રવાહ વહે તો સંયોજનનો સમતુલ્ય પ્રેરણ .......... વડે મળી શકે.View Solution
- 8$ABCDEFA$ લૂપના છ શિરોબિંદુ $\mathrm{A}(0,0,0), \mathrm{B}(5,0,0),$$\mathrm{C}(5,5,0) ,\mathrm{D}(0,5,0), \mathrm{E}(0,5,5)$ અને $\mathrm{F}(0,0,5)$ છે. તે $\overrightarrow{\mathrm{B}}=(3 \hat{\mathrm{i}}+4 \hat{\mathrm{k}}) \;\mathrm{T}$ ધરાવતા ચુંબકીય ક્ષેત્રમાં છે.તો લૂપ $\mathrm{ABCDEFA}$ માથી પસાર થતું ફ્લક્સ ($Wb$ માં) કેટલું હશે?View Solution
- 9એક આદર્શ ટ્રાન્સદોર્મરમાં ગૂંચળાના આંટાઓનો ગુણોત્તર $\frac{N_p}{N_s}=\frac{1}{2}$ છે. ગુણોત્તર $V_s: V_p$ . . . . ને બરાબર થશેં. [સંજ્ઞા તેમના પ્રથાંતત અર્થ રજૂ કરે છે]View Solution
- 10$ 2\Omega $ અવરોધ ધરાવતી આર્મેચર મોટરને $220\, V$ $DC$ સપ્લાય સાથે લગાવવામાં આવે છે,મોટર મહત્તમ ઝડપથી ફરે ત્યારે ઉદ્ભવતો બેક $emf$ $210 \,V$ છે,તો આર્મેચરનો પ્રવાહ કેટલા ........$A$ થશે?View Solution
