$R$ ત્રિજયાના નક્કર ગોળાની અંદર $r$ ત્રિજ્યાનો પોલો ભાગ છે જે લાકડાના વહેરથી ભરેલો છે.નક્કર અને લાકડાના વહેરની સાપેક્ષ ઘનતા $2.4$ અને $0.3$ છે.સંપૂર્ણ કદ પાણીની અંદર હોય તે રીતે ગોળાને તરવા માટે નક્કર અને લાકડાના વહેરના દળનો ગુણોત્તર કેટલો હોવો જોઈએ?
AIIMS 1995, Diffcult
b
(b)Let specific gravities of concrete and saw dust are \({\rho _1}\) and \({\rho _2}\) respectively.
According to principle of floatation weight of whole sphere = upthrust on the sphere
\(\frac{4}{3}\pi ({R^3} - {r^3}){\rho _1}g + \frac{4}{3}\pi {r^3}{\rho _2}g = \frac{4}{3}\pi {R^3} \times 1 \times g\)
==> \({R^3}{\rho _1} - {r^3}{\rho _1} + {r^3}{\rho _2} = {R^3}\)
==> \({R^3}({\rho _1} - 1) = {r^3}({\rho _1} - {\rho _2})\) ==> \(\frac{{{R^3}}}{{{r^3}}} = \frac{{{\rho _1} - {\rho _2}}}{{{\rho _1} - 1}}\)
==> \(\frac{{{R^3} - {r^3}}}{{{r^3}}} = \frac{{{\rho _1} - {\rho _2} - {\rho _1} + 1}}{{{\rho _1} - 1}}\)
==> \(\frac{{({R^3} - {r^3}){\rho _1}}}{{{r^3}{\rho _2}}} = \left( {\frac{{1 - {\rho _2}}}{{{\rho _1} - 1}}} \right)\;\frac{{{\rho _1}}}{{{\rho _2}}}\)
==> \(\frac{{{\rm{Mass of concrete }}}}{{{\rm{Mass of saw dust}}}} = \left( {\frac{{1 - 0.3}}{{2.4 - 1}}} \right) \times \frac{{2.4}}{{0.3}} = 4\)
(b)Let specific gravities of concrete and saw dust are \({\rho _1}\) and \({\rho _2}\) respectively.
According to principle of floatation weight of whole sphere = upthrust on the sphere
\(\frac{4}{3}\pi ({R^3} - {r^3}){\rho _1}g + \frac{4}{3}\pi {r^3}{\rho _2}g = \frac{4}{3}\pi {R^3} \times 1 \times g\)
==> \({R^3}{\rho _1} - {r^3}{\rho _1} + {r^3}{\rho _2} = {R^3}\)
==> \({R^3}({\rho _1} - 1) = {r^3}({\rho _1} - {\rho _2})\) ==> \(\frac{{{R^3}}}{{{r^3}}} = \frac{{{\rho _1} - {\rho _2}}}{{{\rho _1} - 1}}\)
==> \(\frac{{{R^3} - {r^3}}}{{{r^3}}} = \frac{{{\rho _1} - {\rho _2} - {\rho _1} + 1}}{{{\rho _1} - 1}}\)
==> \(\frac{{({R^3} - {r^3}){\rho _1}}}{{{r^3}{\rho _2}}} = \left( {\frac{{1 - {\rho _2}}}{{{\rho _1} - 1}}} \right)\;\frac{{{\rho _1}}}{{{\rho _2}}}\)
==> \(\frac{{{\rm{Mass of concrete }}}}{{{\rm{Mass of saw dust}}}} = \left( {\frac{{1 - 0.3}}{{2.4 - 1}}} \right) \times \frac{{2.4}}{{0.3}} = 4\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક પાત્રમાં પારો ($\rho =13.6\; g cm^{-3}$) અને તેલ ($\rho =0.8 \;g cm^{-3}$) ભરેલા છે.એક ગોળો તેના અડઘું કદ પારામાં અને અડઘું કદ તેલમાં રહે તે રીતે તરે છે. તો ગોળાના દ્રવ્યની ઘનતા $g cm^{-3}$ માં કેટલી હશે?View Solution
- 2View Solutionપ્રવાહીમાં ધાતુનો નાનો ગોળો નાખતાં તેનો વેગ સમય સાથે કયાં આલેખ મુજબ બદલાય છે. ?
- 3View Solutionશ્યાનતા ખેંચાણ બળ શેના પર આધાર રાખે છે?
- 4View Solution'તરલ' શબ્દનો ઉપયોગ શેના માટે કરવામાં આવે છે ?
- 5શિરોલંબ સમતલમાં એક પાતળી નળીને વાળીને $r$ ત્રિજ્યાનું વર્તુળ બનાવવામાં આવે છે.${\rho _1}$ અને ${\rho _2}\left( {{\rho _1} > {\rho _2}} \right)$ ઘનતા ધરાવતા બે સમાન કદબા એકબીજામાં મિશ્ર ના થાય તેવા પ્રવાહી દ્વારા અડધું વર્તુળ ભરેલ છે.શિરોલંબ અને બંને પ્રવાહી મળતા હોય તે સપાટી વચ્ચે વચ્ચેનો ખૂણો $\theta$ કેટલો થાય?View Solution
- 6$A$ ક્ષેત્રફળ ધરાવતા પાત્રમાં પાણી $3\,m$ ઊંચાઈ સુધી પાણી ભરેલ છે.તળીયેથી $52.5\, cm$ ઊંચાઈએ પાત્રની દીવાલમાં $‘A_0’$ ક્ષેત્રફળ ધરાવતું કાણું પાડવામાં આવે છે.જો $A_0/A = 0.1$ હોય તો $v^2$ ........ $m^2/s^2$ થાય. (જ્યાં $v$ એ કાણાંમાથી બહાર આવતા પાણીનો વેગ છે)View Solution
- 7નળાકાર પાત્રમાં પ્રવાહી ભરેલ છે.જયારે પાત્રને તેના અક્ષને અનુલક્ષીને ફેરવવામાં આવે છે.પ્રવાહી તેની બાજુ પર ચડે છે.પાત્રની ત્રિજયા $ r $ અને પાત્રની કોણીય આવૃતિ $\omega $ પરિભ્રમણ/સેકન્ડ છે. કેન્દ્ર અને બાજુ પરના પ્રવાહીની ઊંચાઇનો તફાવત કેટલો થાય?View Solution
- 8View Solutionપદાર્થ પ્રવાહીની સપાટી પર તરે છે. પદાર્થની ઘનતા પ્રવાહીની ઘનતા જેટલી છે.પદાર્થને ધીમેથી નીચે ધકેલવામાં આવે તો ....
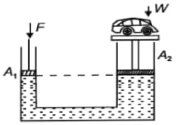
- 9આકૃતિમાં દશાવેલ હાઈડ્રોલિક જેકમાં, કારનું દળ $W=800\,kg , A_1=10 \,cm ^2, A_2=10 \,m ^2$ છે તો કારને ઊંચકવા માટ જરૂરી ન્યૂનતમ બળ $F$ એ .......... $N$ છે?View Solution
- 10$20 \,m$ પાણીની સપાટીની નીચે તરવૈયા ઉપર લાગતું દબાણ ............. $atm$View Solution
