સ્લિટ દ્વારા થતા ફ્રોનહોફર વિવર્તનમાં, જો સ્લીટની પહોળાઈ $a$, તરંગલંબાઈ $\lambda$, અને લેન્સની કેન્દ્રલંબાઈ $f$ હોય તો કેન્દ્રીય મહત્તમની રેખીય પહોળાઈ.....
Easy
Download our app for free and get started
c
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1સિંગલ સ્લીટ વિવર્તનના પ્રયોગમાં મુખ્ય મધ્યમાન શલાકાની તીવ્રતા ${I_0}$ હોય તો સ્લીટની પહોળાઈ બમણી કરવામાં આવે તો તીવ્રતા કેટલી થાય?View Solution
- 2યંગના પ્રયોગમાં બે સ્લિટ વચ્ચેનું અંતર $d = \lambda /4$ છે,ઉપયોગમાં લીઘેલ પ્રકાશની તરંગલંબાઇ $\lambda$ છે શરુઆતનો કળાતફાવત $ \pi/4$ છે. તો $\theta = 30^o$ આગળ તીવ્રતા કેટલી થાય?View Solution
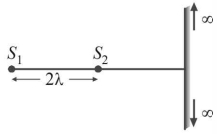
- 3બે સ્ત્રોતને $2 \lambda$ જેટલા અંતરે રાખેલ છે. એક મોટી સ્ક્રીન તેમનો જોડતી રેખાથી લંબ છે. ( $\lambda=$ પ્રકાશની તરંગલંબાઈ) સ્ક્રીન પરના મહત્તમની સંખ્યા ........View Solution
- 4યંગના બે-સ્લિટનાં પ્રયોગમાં, જ્યારે $600\,nm$ તરંગલંબાઈનો પ્રકાશાનો ઉપયોગ કરવામાં આવે છે, ત્યારે એક વિદ્યાર્થી પડદાના ચોક્કસ ભાગમાં $8$ શાલાકાઓ જુએ છે. જો પ્રકાશની તરંગલંબાઈ બદલીને $400\,nm$ કરવામાં આવે તો પડદાના તે જ ભાગમાં હવે તેને જોવા મળતી શલાકાઓની સંખ્યા$....$હશે.View Solution
- 5સમતલ કાચની પ્લેટ ઉપર સમતલ બહિર્ગોળ લેન્સની બહિર્ગોળ સપાટી મૂકીને હવાની પાતળી ફિલ્મ (સ્તર) રચેલ છે. એકરંગી પ્રકાશ સાથે આ પાતળી ફિલ્મ સૌથી ઉપરની બહિર્ગોળ સપાટી અને નીચેની કાચની સપાટી પરથી થતા પરાવર્તનના લીધે વ્યતિકરણ રચના આપે છે.View Solution
વિધાન : $1$ : જ્યારે પ્રકાશ હવા -કાચની પ્લેટમાંથી પરાવર્તિત થઈને વ્યતિકરણ પામે છે. તો પરાવર્તિત તરંગ જેટલો કળા તફાવત આપે છે.
વિધાન : $2$: વ્યતિકરણ ભાતનું કેન્દ્ર અપ્રકાશિત છે.
- 6View Solutionવ્યતિકરણની ઘટના ઉપજાવવા માટે આપણે એવા બે ઉદ્દગમની જરૂર પડે છે જે ......નું વિકીરણ ઉત્સર્જીત કરે.
- 7View Solutionફેશનલ બાયપ્રિઝમ ના પ્રયોગમાં નીચેનામાંથી ક્યો પ્રકાશ ઉદ્દગમ કેન્દ્રીય શલાકાને દર્શાવવા વાપરવામાં આવે છે?
- 8View Solutionગૌણ તરંગોનો હાઈગેંસનો વિચાર
- 9View Solutionહવાથી ભરેલી ચેમ્બરમાં વ્યતિકરણની ઘટનાનું અવલોકન કરવામાં આવે છે, હવે સમગ્ર ચેમ્બરને શૂન્યાવકાશિત કરવામાં આવે અને તે જ પ્રકાશનો ઉપયોગ કરવામાં આવે છે, પછી નિરીક્ષક જોશે કે ......
- 10$1 \;m$ દૂર રહેલી બે સ્લિટને $6.5 \times 10^{-7}\; m$ તરંગલંબાઈના લાલ પ્રકાશ વડે પ્રકાશિત કરવામાં આવે છે. સ્લિટથી $1\;m$ દૂર મૂકલા પડદા પર વ્યતિકરણ શલાકાઓ જોવા મળે છે. કેન્દ્રિય મહતમની સમાન બાજુએ રહેલ ત્રીજી અપ્રકાશિત શલાકા અને પાંચમી પ્રકાશિત શલાકા વચ્ચેનું અંતર કેટલું છે?View Solution