યંગના બે-સ્લિટનાં પ્રયોગમાં, જ્યારે $600\,nm$ તરંગલંબાઈનો પ્રકાશાનો ઉપયોગ કરવામાં આવે છે, ત્યારે એક વિદ્યાર્થી પડદાના ચોક્કસ ભાગમાં $8$ શાલાકાઓ જુએ છે. જો પ્રકાશની તરંગલંબાઈ બદલીને $400\,nm$ કરવામાં આવે તો પડદાના તે જ ભાગમાં હવે તેને જોવા મળતી શલાકાઓની સંખ્યા$....$હશે.
NEET 2022, Medium
Download our app for free and get started
c
\(y=(n \lambda)\left(\frac{D}{d}\right)\)
\(y=(n \lambda)\left(\frac{D}{d}\right)\)
\(n _{1} \lambda_{1}= n _{2} \lambda_{2}\)
\((8)\) \((600 nm )= n _{2}(400)\)
\(n _{2}=12\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1બે તરંગલંબાઈ $2000\;\mathring A$ and $3000 \;\mathring A $ દ્વારા બે માઇક્રોસ્કોપીક કણોનું વિભેદન ${P_A}$ અને ${P_B}$ મળે છે. તો ..View Solution
- 2View Solutionપ્રકાશની તીવ્રતા કોના પર આધારિત છે.
- 3એક પ્રારંભમાં સમાંતર નળાકારીય તરંગો $\mu\,(I)$ = $\mu_0 $+ $\mu_2I$, વક્રીભવનાંકવાળા માધ્યમમાં ગતિ કરે છે. જ્યાં, $\mu_0 $ અને $\mu_2$ એ ઘન અચળાંક છે અને $I$ એ તીવ્રતા છે. તરંગની તીવ્રતા ઘટે તો ત્રિજ્યા વધે છે. તરંગ અગ્રનો પ્રારંભનો આકાર …….View Solution
- 4View Solutionબિંદુવ્ત ઉદ્ગમ અને પડદા વચ્ચેનું અંતર બમણું કરતાં પડદા પર પ્રકાશની તીવ્રતા કેટલા ગણી થાય?
- 5યંગના બે સ્લિટના પ્રયોગમાં, પથ તફાવત $\frac{\lambda}{4}$ અને $\frac{\lambda}{3}$ હોય (પ્રકાશની તરંગ લંબાઈ) તેવા બે બિંદુએ તીવ્રતા અનુક્રમે $I _1$ અને $I _2$ છે. જો $I _0$ પ્રત્યેક સ્લિટમાંથી ઉત્પન્ન થતી પ્રકાશની તીવ્રતા દર્શાવે તો $\frac{I_1+I_2}{I_0}=..........$View Solution
- 6યંગના પ્રયોગમાં પડદા પર શલાકાની પહોળાઈ $0.2 \,mm$ જેટલી છે. જો વ્યતિકરણ ઊપજાવતા પ્રકાશની તરંગલંબાઈમાં $10\%$ જેટલો વધારો કરવામાં આવે અને બે સ્લિટ $S_1$ અને $S_2 $ વચ્ચેના અંતરમાં પણ $10\%$ નો વધારો કરવામાં આવે, તો નવી શલાકાઓની પહોળાઈ .......$mm$ થશે.View Solution
- 7યંગના ડબલ-સ્લિટ પ્રયોગમાં પડદા પરના જે બિંદુએ પથ તફાવત $\lambda $ છે, ત્યાં પ્રકાશની તીવ્રતા $K$ જેટલી છે,$(\lambda$ વપરાયેલ પ્રકાશની તરંગલંબાઇ છે). જે બિંદુએ પથ તફાવત $\frac{\lambda }{4}$ હોય ત્યાં તીવ્રતા કેટલી થાય?View Solution
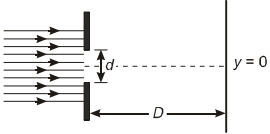
- 8પ્રયોગ માં ઇલેકટ્રોન તેમની દ્-બ્રોગ્લી તરગ્રલંબાઇને સમાન $d$ જાડાઇની નાની સ્લીટમાંથી પસાર થાય છે. તેઓ સ્લીટથી $D$ અંતરે સ્ક્રીન પર જોઇ શકાય છે. નીચેનામાંથી ક્યા આલેખ વડે બતાવી શકાય તથા તે $N$ ઇલેકટ્રોનની સંખ્યા કે જે ડીરેકટર સ્થાન $y$ પર દેખાય તેનું નિર્દશન કરે છે. ($y = 0$ એ સ્લીટની વચ્ચેનું સ્થાન છે.) ?View Solution
- 9View Solutionજો યંગના બે-સ્લિટનાં પ્રયોગમાં વપરાતાં પ્રકાશ ઉદગમ લાલ થી બદલી જાંબલી કરવામાં આવે તો ...... .
- 10$6 \times 10^{-7} \,m$ તરંગલંબાઈ ધરાવતું સમતલ તરંગ-અગ્ર $0.4 \,mm$ પહોળાઈની સ્લિટ પર આપાત કરવામાં આવે છે. સ્લિટની પાછળ $0.8 \,m$ કેન્દ્રલંબાઈનો બહિર્ગોળ લેન્સ મૂકતાં પડદા પર વિવર્તનભાત રચાય છે, તો બીજા અધિકતમની રેખીય પહોળાઈ કેટલા ............$mm$ હશે ?View Solution